- #1
question dude
- 80
- 0
I'm not sure if I've understood my textbook correctly. Can you tell me if my current understanding is correct:
- in a single slit diffraction there's a wide central fringe which is twice as wide as all the other outer fringes
- if we had a double slit diffraction instead of a single slit, we would see fringes within the area that would've been occupied by the wide central fringe
Below is a diagram in my textbook showing intensity distribution of young's fringes, I don't really understand it. Is the blue line supposed to represent the fringes of a single slit diffraction, and the solid red line is representing the fringes of a double slit? I also don't understand at all what the dashed lines in the background are about
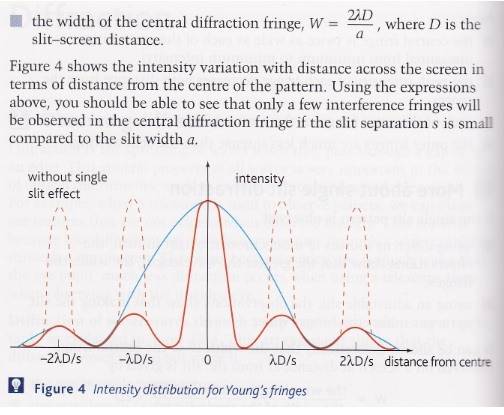
(btw this is all high school level physics)
- in a single slit diffraction there's a wide central fringe which is twice as wide as all the other outer fringes
- if we had a double slit diffraction instead of a single slit, we would see fringes within the area that would've been occupied by the wide central fringe
Below is a diagram in my textbook showing intensity distribution of young's fringes, I don't really understand it. Is the blue line supposed to represent the fringes of a single slit diffraction, and the solid red line is representing the fringes of a double slit? I also don't understand at all what the dashed lines in the background are about
(btw this is all high school level physics)