D_K
- 3
- 0
Hi,
How to determine a threshold aperture, at which the diffraction begins to limit resolution of the sensor ? Which situation reflects that point:
1) Airy disk diameter / 2 = 2 x pixel pitch
http://www.outbackphoto.com/dp_essentials/dp_essentials_02/essay.html"
(third pixel detects the dark gap between two points)
2) Airy disk diameter / 2 = 1 x pixel pitch
3) Airy disk diameter = pixel pitch
it seems that http://en.wikipedia.org/wiki/Airy_disk" , and many webpages
#1 and #2 just meet the http://books.google.pl/books?id=5Yn...nd digital imaging By R. E. Jacobson&f=false", #3 is far further.
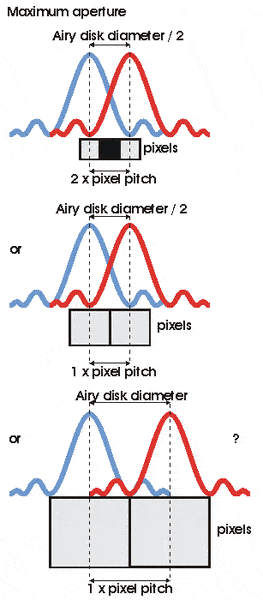
And how to draw such plot:
http://books.google.pl/books?id=5Yn...and digital imaging By R. E. Jacobson&f=false
(Page 80, Fig 6.11)
using software like http://www.padowan.dk/graph/" or eventually Google Charts ? I mean simplified function equation or equations.
Thanks
How to determine a threshold aperture, at which the diffraction begins to limit resolution of the sensor ? Which situation reflects that point:
1) Airy disk diameter / 2 = 2 x pixel pitch
http://www.outbackphoto.com/dp_essentials/dp_essentials_02/essay.html"
(third pixel detects the dark gap between two points)
2) Airy disk diameter / 2 = 1 x pixel pitch
3) Airy disk diameter = pixel pitch
it seems that http://en.wikipedia.org/wiki/Airy_disk" , and many webpages
#1 and #2 just meet the http://books.google.pl/books?id=5Yn...nd digital imaging By R. E. Jacobson&f=false", #3 is far further.
And how to draw such plot:
http://books.google.pl/books?id=5Yn...and digital imaging By R. E. Jacobson&f=false
(Page 80, Fig 6.11)
using software like http://www.padowan.dk/graph/" or eventually Google Charts ? I mean simplified function equation or equations.
Thanks
Attachments
Last edited by a moderator:
