evilbrent
- 4
- 0
Hi,
I'm an engineer designing a spring system for a garage roller door. I need to know the number of turns of the door for all the size combinations.
I've found this page which gives a good equation for finding the length if you know the number of turns, starting radius and gap between spirals:
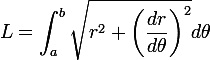
The equation of the spiral is r=x+yθ, so x=starting radius, y=gap/2∏, and to find L we're taking the integral from a=0 to b=2∏n (where n=turns).
When you know n, this is straightfoward, and even I could work that out. But it's been a decade since I've done anything like this, so I was wondering if anyone could help me find an expression for n in this:
L=∫^{2∏n}_{0} \sqrt{(a+bθ)^2+b^2}dθ
Lord help me, my way of solving this is to find L for n=1,2,3,4,5 etc, graph it in excel and use "find trendline" to get an equation. Any help appreciated, thanks.
I'm an engineer designing a spring system for a garage roller door. I need to know the number of turns of the door for all the size combinations.
I've found this page which gives a good equation for finding the length if you know the number of turns, starting radius and gap between spirals:
The equation of the spiral is r=x+yθ, so x=starting radius, y=gap/2∏, and to find L we're taking the integral from a=0 to b=2∏n (where n=turns).
When you know n, this is straightfoward, and even I could work that out. But it's been a decade since I've done anything like this, so I was wondering if anyone could help me find an expression for n in this:
L=∫^{2∏n}_{0} \sqrt{(a+bθ)^2+b^2}dθ
Lord help me, my way of solving this is to find L for n=1,2,3,4,5 etc, graph it in excel and use "find trendline" to get an equation. Any help appreciated, thanks.
Last edited: