- #1
Bin Qasim
why cos 90 is 0??
Hello everyone
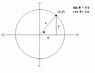
got one question here... why cos 0 is 0?
cos of any angle is adjescent by hypotenuse. so what is adjescent in case of 90 degree angle??
is the question clear? please reply ASAP...pls
thanx in advance...
Hello everyone
got one question here... why cos 0 is 0?
cos of any angle is adjescent by hypotenuse. so what is adjescent in case of 90 degree angle??
is the question clear? please reply ASAP...pls
thanx in advance...