- #1
Gh778
- 421
- 0
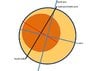
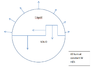
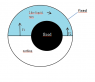
Take half torus with solid part of density 1, other half torus with liquid of density 1. The torus turn at W rd/s enough for maintain liquid at external circle. Now, for 0 to 180° we accelerate torus, this increase forces (blue in drawing) from pressure of water and from 180° to 360° we deccelerate torus. Rotationnal speed change from W to W+w to W. It's like torus change the CG without external forces. I thought solid give pressure too but I can imagine 2 liquids with different density, it's the same. I have some questions:
1/ water don't give pressure so no force exist ?
2/ solid give same pressure ?
3/ when we rotate the forces from rotation, this cancel pressure forces ?
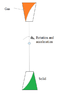
Edit: I add another drawing for show different positions
1/ water don't give pressure so no force exist ?
2/ solid give same pressure ?
3/ when we rotate the forces from rotation, this cancel pressure forces ?
Edit: I add another drawing for show different positions
Attachments
Last edited: