- #1
AntiElephant
- 25
- 0
Apologies if this is rather trivial. I'm having a hard time wrapping my mind around the mathematics of energy bands and periodic potentials.
I understand that an electron in a periodic potential will be of the form [itex] \phi_k(r) = e^{ik.r}u_k(r) [/itex]. This wavefunction has periodicity of the reciprocal lattice and so the same is true for any physical observable of the electron, such as its energy. However my confusion comes in with the introduction of energy bands.
My book begins off with the introduction of a weak periodic potential to illustrate the formation of band gaps at brillouin zone boundaries (perp. bisectors of a certain reciprocal lattice vector), and how far away from these boundaries there are two energy solutions corresponding to the free electron energies of wavevectors [itex] k [/itex] and [itex] k + G [/itex], G being the reciprocal lattice vector for the previous zone boundary.
This summarises the findings, Vg being low than the free-electron terms (E^0 denotes free-electron energy) corresponds to not being near the zone boundary.
http://img405.imageshack.us/img405/1456/40946286.png
But how does this any of this tie in with periodicity of the energy in k-space? What does it mean to have two energy eigenvalues for the same k-state? Can I have two electrons occupying the exact same state but in different energy levels? And if far away from a zone boundary of the recip. lattice vector G there correspond to two solutions, then surely there would actually correspond an infinite number of solutions for a specific k because you would be far away from the zone boundary for every recip. lattice vector G.
This;
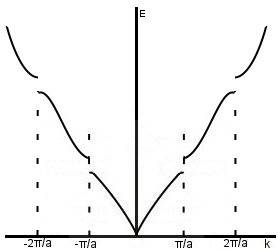
presents a formulation of the equation above, but it doesn't have periodicity and there doesn't seem to correspond two "solutions" (or infinite if what I said before was correct) to a particular k-value as the equations before showed. I'm honestly confused with what the equations above are trying to explain in relation to band-theory.
How can we talk of periodicity in the energy if the weak periodic potential gives a form of electron energy as shown that diagram above? What is the physical significance of two energy solutions for a particular k-value?
I understand that an electron in a periodic potential will be of the form [itex] \phi_k(r) = e^{ik.r}u_k(r) [/itex]. This wavefunction has periodicity of the reciprocal lattice and so the same is true for any physical observable of the electron, such as its energy. However my confusion comes in with the introduction of energy bands.
My book begins off with the introduction of a weak periodic potential to illustrate the formation of band gaps at brillouin zone boundaries (perp. bisectors of a certain reciprocal lattice vector), and how far away from these boundaries there are two energy solutions corresponding to the free electron energies of wavevectors [itex] k [/itex] and [itex] k + G [/itex], G being the reciprocal lattice vector for the previous zone boundary.
This summarises the findings, Vg being low than the free-electron terms (E^0 denotes free-electron energy) corresponds to not being near the zone boundary.
http://img405.imageshack.us/img405/1456/40946286.png
But how does this any of this tie in with periodicity of the energy in k-space? What does it mean to have two energy eigenvalues for the same k-state? Can I have two electrons occupying the exact same state but in different energy levels? And if far away from a zone boundary of the recip. lattice vector G there correspond to two solutions, then surely there would actually correspond an infinite number of solutions for a specific k because you would be far away from the zone boundary for every recip. lattice vector G.
This;
presents a formulation of the equation above, but it doesn't have periodicity and there doesn't seem to correspond two "solutions" (or infinite if what I said before was correct) to a particular k-value as the equations before showed. I'm honestly confused with what the equations above are trying to explain in relation to band-theory.
How can we talk of periodicity in the energy if the weak periodic potential gives a form of electron energy as shown that diagram above? What is the physical significance of two energy solutions for a particular k-value?
Last edited by a moderator: