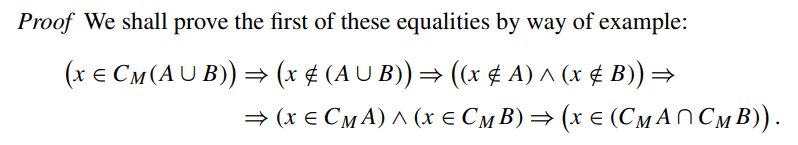SUMMARY
The discussion centers on the necessity of De Morgan's laws for sets in a specific proof involving the expression $$x\in C_M(A\cup B)\iff x\notin(A\cup B)$$. Participants confirm that the predicates are indeed equivalent and clarify the correct use of LaTeX formatting for mathematical expressions. The consensus is that the implications presented are two-way, reinforcing the validity of the equivalence in the context of set theory.
PREREQUISITES
- Understanding of set theory concepts, specifically union and membership.
- Familiarity with De Morgan's laws as they apply to sets.
- Basic knowledge of logical implications and equivalences.
- Proficiency in LaTeX for formatting mathematical expressions.
NEXT STEPS
- Study De Morgan's laws in detail to understand their application in set theory.
- Learn about logical implications and how to prove equivalences in mathematics.
- Practice using LaTeX for mathematical notation to enhance clarity in proofs.
- Explore advanced topics in set theory, such as Cartesian products and power sets.
USEFUL FOR
Mathematicians, students of mathematics, and educators looking to deepen their understanding of set theory and logical implications in proofs.