Hello BBandaRR,
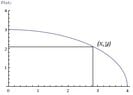
5.) I am assuming we wish to maximize the area of the resulting rectangle. By the symmetry of the ellipse and thus the inscribed rectangle, we need only concern ourselves with the first quadrant. So, let's first draw a diagram:
View attachment 1259
The area $A$ of the rectangle is our objective function:
$$A(x,y)=xy$$
subject to the constraint:
$$g(x,y)=9x^2+16y^2-144=0$$
Using a single-variable method, we may solve the constraint for either variable, and then substitute into the objective function to get the area as a function of one variable, and then use differentiation to find the maximum value. However, if we observe that maximizing the square of the area function times some constant is equivalent to maximizing the area itself, we may make our computations of the derivatives much simpler. So let us write:
$$\left(4A(x,y) \right)^2=f(x,y)=x^2\left(16y^2 \right)$$
By the constraint, we have:
$$16y^2=144-9x^2$$
and so we may write:
$$f(x)=x^2\left(144-9x^2 \right)=144x^2-9x^4$$
Differentiating with respect to $x$, and equating the result to zero, we find:
$$f'(x)=288x-36x^3=36x\left(8-x^2 \right)=0$$
Since $x$ must be non-negative, we have the two critical values:
$$x=0,\,2\sqrt{2}$$
Computing the second derivative, we find:
$$f''(x)=288-108x^2$$
And so we know the critical value $x=0$ is associated with a minimum and the critical value $x=2\sqrt{2}$ is associated with a maximum.
Thus, for this value of $x$, we find:
$$y=\sqrt{\frac{144-9\cdot8}{16}}=\frac{3}{\sqrt{2}}$$
Now, using the fact that we wish to include all 4 quadrants in our final answer, this means we need to double $x$ and $y$ to find the dimensions of the rectangle of largest area that can be inscribed withing the given ellipse.
Hence, the width $w$ of the rectangle is:
$$w=2x=4\sqrt{2}$$
and the height $h$ of the rectangle is:
$$h=2y=\frac{6}{\sqrt{2}}=3\sqrt{2}$$
Our result would seem to suggest that the ratio of the width to the height of the rectangle is equal to the ratio of the length of the horizontal axis to the vertical axis of the ellipse in which the rectangle is inscribed.
Let's prove this conjecture using Lagrange multipliers. We have the objective function:
$$A(x,y)=xy$$
subject to the constraint:
$$g(x,y)=b^2x^2+a^2y^2-a^2b^2=0$$
Note: the constraint is derived from $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$.
And so, we obtain the following system:
$$y=\lambda\left(2b^2x \right)$$
$$x=\lambda\left(2a^2y \right)$$
This implies:
$$\lambda=\frac{y}{2b^2x}=\frac{x}{2a^2y}\implies \frac{x}{y}=\frac{a}{b}$$
Thus, our conjecture is true. Substitution into the constraint will yield the dimensions of the rectangle:
$$w=2x=\sqrt{2}a$$
$$h=2y=\sqrt{2}b$$
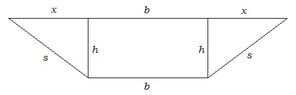
Problems 6.) and 7.) can both be solved by developing one theorem, that is to maximize the area of an isosceles trapezoid, given the base and the length of the slanted sides. Let's begin by drawing a diagram:
View attachment 1260
And so our objective function is:
$$A(h,x)=\frac{1}{2}(b+2x+b)h=(b+x)h$$
subject to the constraint:
$$g(h,x)=x^2+h^2-s^2=0$$
Solving the constraint for $h$, we find:
$$h=\sqrt{s^2-x^2}$$
And so we may write the objective function in one variable $x$:
$$A(x)=(b+x)\sqrt{s^2-x^2}$$
Now, again we may observe that maximizing the square of the area function will maximize the area function itself, and so we may write:
$$A^2(x)=f(x)=(b+x)^2\left(s^2-x^2 \right)$$
Differentiating with respect to $x$, and equating to zero, we find:
$$f'(x)=(b+x)^2(-2x)+\left(s^2-x^2 \right)2(b+x)=-2(b+x)\left(2x^2+bx-s^2 \right)=0$$
The only valid critical value (given that $0<x$) is obtained from the quadratic formula:
$$x=\frac{-b+\sqrt{b^2+8s^2}}{4}$$
The first derivative test shows that this critical value is associated with a maximum, if we observe that the factor $x+b$ must be positive, and the factors $-2\left(2x^2+bx-s^2 \right)$ are a parabola opening downward, and so is positive to the left of the larger root and negative to the right of this root.
Thus, the width $w$ across the top is:
$$w=b+2x=b+\frac{-b+\sqrt{b^2+8s^2}}{2}=\frac{b+\sqrt{b^2+8s^2}}{2}$$
So, for problem 6.) we have:
$$b=16\text{ cm},\,s=8\text{ cm}$$
Hence:
$$w=\frac{16+\sqrt{16^2+8\cdot8^2}}{2}\text{ cm}=8\left(1+\sqrt{3} \right)\text{ cm}$$
And for problem 7.) we have:
$$b=14\text{ cm},\,s=4\text{ cm}$$
Hence:
$$w=\frac{14+\sqrt{14^2+8\cdot4^2}}{2}\text{ cm}=16\text{ cm}$$