Doubt about Jacobi's diagonalization method

[Cloruro de potasio]

TL;DR

Number of iterations required in the Jacobi symmetric matrix diagonalization method

Good Morning,

I am using the Jacobi diagonalization method for symmetric matrices and I have realized that as the number of iterations progresses, the speed with which the larger element (in absolute value) outside the diagonal of the diagonal becomes smaller Matrices are increasing (graphical attachment showing the logarithm of the value of the maximum element (in absolute value) of the matrix together depending on the number of iteration.

I don't understand very well why this happens, can someone help me?

Thank you very much in advance and greetings

 

[QuantumQuest]

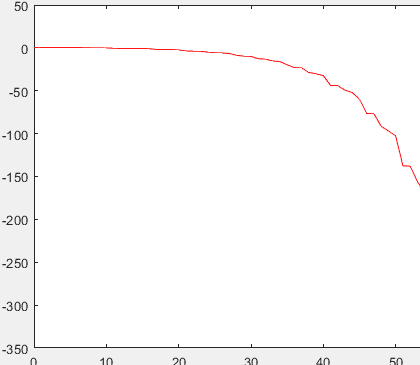
The Jacobi method of matrix diagonalization has a slow convergence. The method is an iterative one and for reducing a $n$ - dimensional symmetric matrix to a diagonal one, it requires a number of iterations proportional to $n$. Now, in each iteration, the number of off-diagonal elements to be annihilated is proportional to $n^2$ - i.e. we have an order of $n^3$ operations. The annihilation of one pair of off-diagonal elements affects the values of others in the same column and row. So, matrix elements that have been put to zero in some operation may become non-zero later on, when another pair is being reduced.

 

[Cloruro de potasio]

Thank you very much,

I understand that the number of iterations is proportional to the size of the matrix to be diagonalized, but ... why does the rate of decrease of the largest element outside the diagonal increase as the number of iterations increases?

 

[QuantumQuest]

but ... why does the rate of decrease of the largest element outside the diagonal increase as the number of iterations increases?

Because it goes to convergence depending on the number of iterations but at a slow rate in general.