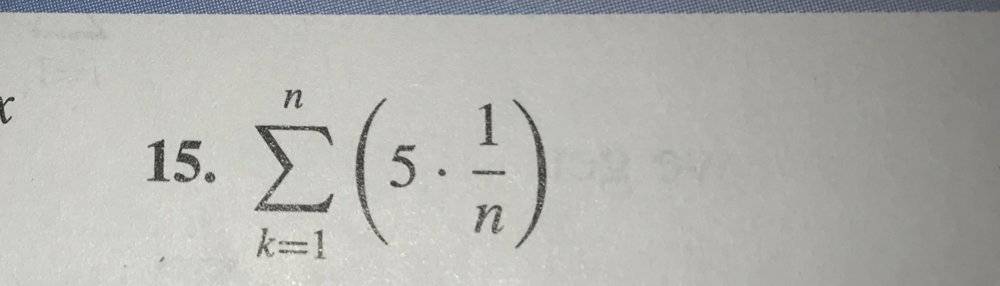Evaluating a Sum: Understanding the Solution

  • Thread starter Thread starter martina1075
  • Start date Start date
  • Tags Tags
    Sum
Click For Summary

Homework Help Overview

The discussion revolves around evaluating a sum, specifically focusing on the interpretation of the summation index and the resulting value. Participants are trying to understand how the answer of 5 is derived from the given problem.

Discussion Character

  • Exploratory, Assumption checking, Problem interpretation

Approaches and Questions Raised

  • Participants are questioning the role of the index in the summation and whether the sum should be evaluated over n or k. There are attempts to clarify how the summation leads to the answer of 5, with some suggesting to test specific values for n.

Discussion Status

There is an ongoing exploration of the assumptions behind the problem, with various interpretations being discussed. Some participants have offered guidance on evaluating the sum and have pointed out potential misunderstandings regarding the index of summation.

Contextual Notes

Participants note that the problem does not explicitly state the stopping point for the index, leading to confusion. There is also mention of a textbook reference for common arithmetic series, though some participants believe it may not be necessary for this problem.

martina1075
Messages
7
Reaction score
0
Homework Statement
Good morning,
can someone help me solve this please?
Thank you in advance
Relevant Equations
As per picture
Cannot conclude the answer
936F78D9-B45A-4B3B-B927-78D9A73E9FE2.jpeg
 
Last edited by a moderator:
Physics news on Phys.org
That's an interesting one. Does it say what you are supposed to do?
 
PeroK said:
That's an interesting one. Does it say what you are supposed to do?
It says to evaluate the sum. The answer should be 5. The problem is how he got to 5.
 
martina1075 said:
It says to evaluate the sum. The answer should be 5. The problem is how he got to 5.

Have you tried with one or two values for ##n## to see what you get?
 
I don't understand. Where is k in the sum? Shouldn't the sum be over n?

1571405718298.png
 
  • Like
Likes   Reactions: Delta2 and SammyS
if I tell you to evaluate $$\sum_{k=1}^n c$$ where c is some constant that does not depend on k(but might depend on other things like n for example) what will your answer be?
 
  • Like
Likes   Reactions: FactChecker and PeroK
berkeman said:
I don't understand. Where is k in the sum? Shouldn't the sum be over n?

View attachment 251393
That's what I thought at first, hence post #2. But, then, I saw the light!
 
  • Like
Likes   Reactions: berkeman
There should be a table in your textbook for common arithmetic series. There is no way that the answer is 5.
 
osilmag said:
There should be a table in your textbook for common arithmetic series. There is no way that the answer is 5.

Read the question carefully!
 
  • #10
osilmag said:
There should be a table in your textbook for common arithmetic series.
No table is needed.
osilmag said:
There is no way that the answer is 5.
See Delta2's hint in post 6.
 
  • #11
PeroK said:
Read the question carefully!

I did!

Five is if the index stops at one. It doesn't state that in the problem, but it sure tricked me.
 
  • #12
osilmag said:
I did!

Five is if the index stops at one. It doesn't state that in the problem, but it sure tricked me.

The answer is ##5## for any value of ##n##.
 
  • #13
PeroK said:
Read the question carefully!
osilmag said:
I did!
Read it even more carefully!
osilmag said:
Five is if the index stops at one. It doesn't state that in the problem, but it sure tricked me.
If n = 2, we have
$$\sum_{k = 1}^2 5 \cdot \frac 1 2 = 5 \cdot \frac 1 2 + 5 \cdot \frac 1 2 = ?$$

What if n = 3? What if n = 4?
 
  • #14
Ok. I got it! Like I said it tricked me.

I had thought the index counted up from k to n.
 
  • #15
osilmag said:
Ok. I got it! Like I said it tricked me.

I had thought the index counted up from k to n.
No, the index k counts up from 1 to n. Since the summand doesn't involve k, and so is constant, we're just adding ##5 \cdot \frac 1 n## n times.
 
  • #16
Mark44 said:
No, the index k counts up from 1 to n. Since the summand doesn't involve k, and so is constant, we're just adding ##5 \cdot \frac 1 n## n times.

... which is essentially the definition of ##n \times \frac 5 n##.
 
  • #17
PeroK said:
... which is essentially the definition of ##n \times \frac 5 n##.
But is not the usual definition of "5"!
 

Similar threads

What is the formula for finding the nth partial sum?
  • · Replies 15 ·
Replies
15
Views
2K
Find the sum of the coefficients in the expansion ##(1+x)^n##
  • · Replies 5 ·
Replies
5
Views
2K
Every integer greater than 5 is the sum of three primes?
  • · Replies 4 ·
Replies
4
Views
4K
Show that the sum of twin primes ## p ## and ## p+2 ## is divisible?
  • · Replies 17 ·
Replies
17
Views
3K
Game theory: dice game to aim for sum no greater than 9
  • · Replies 11 ·
Replies
11
Views
4K
Trying to find an easier way to compute the double sum
  • · Replies 7 ·
Replies
7
Views
2K
Find the sum of the coefficients of ##(x+y)^{16}##
  • · Replies 5 ·
Replies
5
Views
1K
Undergrad Evaluation of the sum 1^m+3^m+5^m+ ....................(2n+1)^{m}
  • · Replies 1 ·
Replies
1
Views
2K
Evaluating Sum from j=1 to n: i=k
  • · Replies 2 ·
Replies
2
Views
1K
Finding a and d from the Sum of an Arithmetic Series
  • · Replies 2 ·
Replies
2
Views
2K