SUMMARY
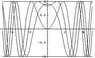
The differential equation dy/dx = x(1 - y^2)^(1/2) requires finding singular solutions in addition to the general solution. Singular solutions, such as y(x) = 1 and y(x) = -1, envelop the general solutions derived from separating variables and integrating. The discussion emphasizes the importance of visualizing these solutions through plotting, which clarifies the relationship between general and singular solutions. A plot illustrating y(x) = sin(x^2/2 + c) alongside the singular solutions effectively demonstrates this concept.
PREREQUISITES
- Understanding of differential equations, particularly first-order non-linear equations.
- Knowledge of separation of variables and integration techniques.
- Familiarity with the concept of singular solutions in differential equations.
- Basic skills in plotting functions to visualize solutions.
NEXT STEPS
- Study the concept of singular solutions in differential equations.
- Learn how to separate variables and integrate first-order non-linear equations.
- Explore graphical methods for visualizing general and singular solutions.
- Investigate specific examples of singular solutions in other differential equations.
USEFUL FOR
Mathematicians, students studying differential equations, and educators seeking to enhance their understanding of singular solutions and their graphical representations.