chikis
- 236
- 1
Homework Statement
A simple measuring device is used at point X and Y on the same horizontal level to measure the angles of elevation of the peak P of a certain mountain. If X is known to be 5,200m above sea level, |XY| = 4,000m and the measurement of the angles of elevation of P at X and Y are 15¤ and 35¤ respectively, find the height of the mountain. (take tan 15¤ = 0.3 and tan 35¤ = 0.7)
Homework Equations
Tan¤ = opp/adj
The Attempt at a Solution
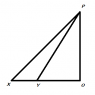
I drew a large triangle XPY which consist of two small triangles, XPO and POY.
The distance |XY| is 4000m. |XY| is above sea level of heigt 5,200m.
The height am required to calculate is the distance |OP|. Let |OP|= h.
We need to find the distance XO and OY respectively. Let XO = (4000-b) and OY = b. Considering triangle XPO, tan15 = h/(4000-b)
---> (4000-b)0.3 = h
1200-0.3b = h
b = 1200-h/0.3 ----->(1)
Considering triangle POY tan35¤ = h/b
h = btan35¤
---> h = 0.7b
b = h/0.7 ----->(2)
Equating equation 1 and 2, you will have:
1200-h/0.3 = h/0.7
840 - 0.7h = 0.3h
0.7h + 0.3h = 840m
h = 840m
the height of the mountian will now become 840m +5,200m
= 6040m
but my answer is not the same as the answer provided for the working. How do I approach this problem?