Find the number of arrangements possible

[Amad27]

The Annual Interplanetary Mathematics Examination (AIME) is written by a committee of five Martians, five Venusians, and five Earthlings. At meetings, committee members sit at a round table with chairs numbered from $1$ to $15$ in clockwise order. Committee rules state that a Martian must occupy chair $1$ and an Earthling must occupy chair $15$, Furthermore, no Earthling can sit immediately to the left of a Martian, no Martian can sit immediately to the left of a Venusian, and no Venusian can sit immediately to the left of an Earthling. The number of possible seating arrangements for the committee is $N(5!)^3$. Find $N$.

We have a race: $M_1 M_2 M_3 M_4 M_5$, the number of arrangements within a race $5!$ arrangements.

Not Possible Arrangements: $EM, VM, VE$.

We start with $M$ and end with an $E$.

If we look carefully, we can put: $MEV$ or $MMEEVV$ but not $MVE$

So it is possible to have:

$MMMMMEEEEEVVVVV$ or $MEVMEVMEVMEVMEVMEV$

But this isn't helpful at all.

 

[johng1]

I don't see how to count this by hand, but the machine is perfectly happy to do so in "zero" seconds. The answer is N = 346. Here's a Java program that computes N:

/*
 The Annual Interplanetary Mathematics Examination (AIME) is written by a committee of five Martians, five
 * Venusians, and five Earthlings. At meetings, committee members sit at a round table with chairs numbered
 * from 0 to 14 in clockwise order. Committee rules state that a Martian must occupy chair 0 and an Earthling
 * must occupy chair 14, Furthermore, no Earthling can sit immediately to the left of a Martian, no Martian can
 * sit immediately to the left of a Venusian, and no Venusian can sit immediately to the left of an Earthling.
 * The number of possible seating arrangements for the committee is N(5!)^3. Find N.
 *  Let E, M and V denote earthling, venusian and martian.  The seat number i+1 is the seat to the left of i
 * Then for 2 cosecutive seats, ME, VM and EV are disallowed.
 * So the valid 2 seats are EE. EM, VV, VE, MM, MV
 */
package seatings;

/**
 *
 * @author John
 */
public class Seatings {

   public static void main(String[] args) {
      FindSeats test = new FindSeats();
      System.out.println("Total number of seatings: " + test.solutions());
      System.out.println("Here are the first 10 found:");
      int i, j;
      for (i = 0; i < 10; i++) {
         for (j = 0; j < 15; j++) {
            System.out.print(test.allSolutions[i][j]);
         }
         System.out.println();
      }
   }
}
package seatings;

public class FindSeats {

   char[] seats;
   char[][] allSolutions;
   int solutionCount;

   FindSeats() {
      seats = new char[15];
      seats[0] = 'M';
      seats[14] = 'E';
      allSolutions = new char[346][15];
      solutionCount = 0;
   }

   private boolean checkSolution() {
      int mCount = 0, vCount = 0, eCount = 1;
      int i;
      for (i = 13; i >= 0; i--) {
         switch (seats[i + 1]) {
            case 'M':
               if (seats[i] == 'V') {
                  return (false);
               }
               if (seats[i] == 'M') {
                  mCount++;
               } else {
                  eCount++;
               }
               break;
            case 'E':
               if (seats[i] == 'M') {
                  return (false);
               }
               if (seats[i] == 'E') {
                  eCount++;
               } else {
                  vCount++;
               }
               break;
            case 'V':
               if (seats[i] == 'E') {
                  return (false);
               }
               if (seats[i] == 'M') {
                  mCount++;
               } else {
                  vCount++;
               }
               break;
         }
      }
      return (mCount == 5 && eCount == 5 && vCount == 5);
   }

   void findSolution(int i, int mCount, int eCount, int vCount) {
      int j;
      if (i == 0) {
         if (seats[1] != 'E') {
            // make certain this is actually a solution
//            if (!checkSolution()) {
//               System.out.println("oops");
//            }
            for (j = 0; j < 15; j++) {
               allSolutions[solutionCount][j] = seats[j];
            }
            solutionCount++;
         }
         return;
      }
      if (seats[i + 1] == 'E') {
         if (eCount > 0) {
            seats[i] = 'E';
            findSolution(i - 1, mCount, eCount - 1, vCount);
         }
         if (vCount > 0) {
            seats[i] = 'V';
            findSolution(i - 1, mCount, eCount, vCount - 1);
         }
      } else if (seats[i + 1] == 'M') {
         if (mCount > 0) {
            seats[i] = 'M';
            findSolution(i - 1, mCount - 1, eCount, vCount);
         }
         if (eCount > 0) {
            seats[i] = 'E';
            findSolution(i - 1, mCount, eCount - 1, vCount);
         }
      } else { // seats[i+1] == 'V'
         if (vCount > 0) {
            seats[i] = 'V';
            findSolution(i - 1, mCount, eCount, vCount - 1);
         }
         if (mCount > 0) {
            seats[i] = 'M';
            findSolution(i - 1, mCount - 1, eCount, vCount);
         }
      }
   }

   int solutions() {
      findSolution(13, 4, 4, 5);
      return (solutionCount);
   }
}

Here's the output of the above program:
Total number of seatings: 346
Here are the first 10 found:
MMMMMVVVVVEEEEE
MVEMMMMVVVVEEEE
MMVEMMMVVVVEEEE
MMMVEMMVVVVEEEE
MMMMVEMVVVVEEEE
MVVEMMMMVVVEEEE
MMVVEMMMVVVEEEE
MMMVVEMMVVVEEEE
MMMMVVEMVVVEEEE
MVVVEMMMMVVEEEE

 

[Opalg]

The Annual Interplanetary Mathematics Examination (AIME) is written by a committee of five Martians, five Venusians, and five Earthlings. At meetings, committee members sit at a round table with chairs numbered from $1$ to $15$ in clockwise order. Committee rules state that a Martian must occupy chair $1$ and an Earthling must occupy chair $15$, Furthermore, no Earthling can sit immediately to the left of a Martian, no Martian can sit immediately to the left of a Venusian, and no Venusian can sit immediately to the left of an Earthling. The number of possible seating arrangements for the committee is $N(5!)^3$. Find $N$.

johng's answer spurs me to have another go at this problem, but I get a different result from his. Edit. After doing this, I see that johng has amended his answer, which now agrees with mine!

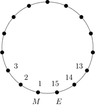
The first difficulty is to understand what the problem tells us about the seating arrangement. The places around the table are numbered from $1$ to $15$ clockwise, with an $M$ in place $1$ and an $E$ in place $15$, like this:

View attachment 4589

​

Notice that the $M$ in place $1$ has an $E$ to his/her/its right, but is not allowed to have an $E$ on the left. So if we list the occupants of places $1$ to $15$ in order, in the form $M\ldots E$, the consecutive pair $ME$ must not occur. In the same way, the pairs $VM$ and $EV$ are forbidden.

To list the possible seating arrangements, start by thinking about how the $M$s are distributed. One possibility is that they all sit together in places $1$ to $5$. For the remaining places, we can never have an $E$ followed by a $V$, so all the $V$s must come first, leading to the unique arrangement $MMMMMVVVVVEEEEE$.

At the other extreme, suppose all the $M$s are separated: $M\ldots M\ldots M\ldots M\ldots M\ldots E$. Each of the gaps must start with a $V$ and end with an $E$. This again leads to a unique arrangement $MVEMVEMVEMVEMVE$.

To list other arrangements, we have to consider all the possible partitions of the five $M$s. The partitions of $5$ are $(1\,1\,1\,1\,1)$, $(2\,1\,1\,1)$, $(2\,2\,1)$, $(3\,1\,1)$, $(3\,2)$, $(4\,1)$ and $(5)$. The first and last of these are covered in the previous two paragraphs.

Next comes the partition $MM\ldots M\ldots M\ldots M\ldots E$. In this arrangement, each group of $M$s must be followed by at least one $V$ and preceded by at least one $E$. So the arrangement looks like $MMV\_\,EMV\_\,EMV\_\,EMV\_\,E$, where each of the underscored spaces consists of $0$ or more $V$s followed by $0$ or more $E$s. There are $4^3=64$ such arrangements ($4$ ways of choosing where the double $M$ comes, $4$ places where the fifth $V$ can be inserted and $4$ places where the fifth $E$ can be inserted).

For the partition $MM\ldots MM\ldots M\ldots E$, the arrangement looks like $MMV\_\,EMMV\_\,EMV\_\,E$, with $3$ ways to distribute the $M$s, $6$ ways to distribute the $V$s into the gaps, and also $6$ ways to distribute the $E$s. That gives a total of $108$ arrangements.

Similarly, for distributions of the form $MMMV\_\,EMV\_\,EMV\_\,E$ there are again $3\times 6\times 6 = 108$ arrangements. For distributions of the form $MMMV\_\,EMMV\_\,E$ there are $2\times 4\times 4 = 32$ arrangements, and for those of the form $MMMMV\_\,EMV\_\,E$ there are again $2\times 4\times 4 = 32$ arrangements.

Adding all those, I make the total number $1+1+108+108+64+32 +32= 346$ arrangements.

 

[johng1]

Well done, OpalG! Just for fun, I thought about extending the problem so that each planet sends k delegates to the conference. It was a simple matter to tweak my program so that the number of arrangements for k delegates is found. Here's some output from the tweaked program:

delegate count 2 has solutions: 2
delegate count 3 has solutions: 10
delegate count 4 has solutions: 56
delegate count 5 has solutions: 346
delegate count 6 has solutions: 2252
delegate count 7 has solutions: 15184
delegate count 8 has solutions: 104960
delegate count 9 has solutions: 739162
delegate count 10 has solutions: 5280932
delegate count 11 has solutions: 38165260
delegate count 12 has solutions: 278415920

My simple minded recursive method starts to bog down with k=12 delegates. The above took 37 seconds on my PC to execute. OpalG's "stars and bars" counting method for the larger delegate counts is not accessible to me.

 

[Opalg]

Just for fun, I thought about extending the problem so that each planet sends k delegates to the conference. It was a simple matter to tweak my program so that the number of arrangements for k delegates is found. Here's some output from the tweaked program:

delegate count 2 has solutions: 2
delegate count 3 has solutions: 10
delegate count 4 has solutions: 56
delegate count 5 has solutions: 346
delegate count 6 has solutions: 2252
delegate count 7 has solutions: 15184
delegate count 8 has solutions: 104960
delegate count 9 has solutions: 739162
delegate count 10 has solutions: 5280932
delegate count 11 has solutions: 38165260
delegate count 12 has solutions: 278415920

The OEIS indicates that this sequence is given by the formula $$S(n) = \sum_{k=0}^n {n\choose k}^{\!\!3}$$, where $S(n)$ is the number of solutions for delegate count $n$.

Given that formula, we ought to able to see some clever way to prove it!