Discussion Overview
The discussion revolves around finding the minimum value of a cost function that depends on two variables, x and y. Participants explore methods for determining the optimal values of these variables through calculus, particularly using partial derivatives and critical points.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
- Debate/contested
Main Points Raised
- One participant describes a cost calculation formula involving two variables and seeks to find the minimum cost values for x and y.
- Another participant requests the specific function and work done so far to provide more targeted assistance.
- There is a discussion about setting the first partial derivatives to zero to find critical points and whether these points represent minimum or maximum values.
- Participants discuss the second derivative test and the Hessian matrix as methods to determine the nature of the critical points.
- One participant expresses a need to confirm that substituting the found values of x and y into the original cost equation will yield the minimum cost.
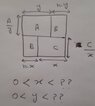
- There is a request for help in determining the range of x and y values that would yield a solution, referencing a figure that is not clearly understood by others.
- Participants express confusion regarding the figure and suggest that the question about the figure may be a separate issue from the original problem.
Areas of Agreement / Disagreement
Participants generally agree on the methods for finding critical points and testing for minima or maxima, but there is no consensus on the clarity of the figure presented or its relevance to the original cost calculation problem.
Contextual Notes
The discussion includes limitations related to the clarity of the visual aids provided and the definitions of variables used in the context of the problem.