Finding ##S_x## eigenstate using experiments

[Kashmir]

Quantum mechanics, McIntyre, pg 62

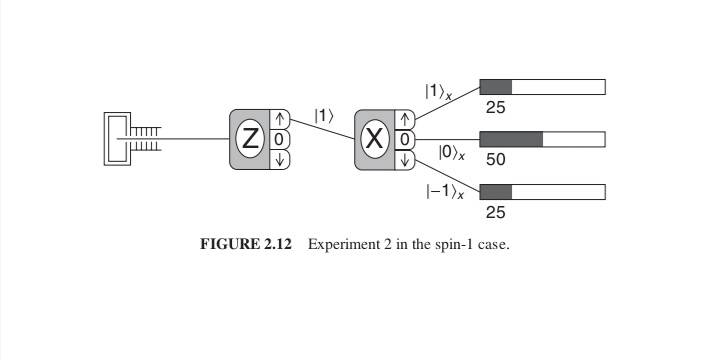
For above spin $1$ Stern Gerlach experiment a set of results is
"$\begin{array}{c} \mathcal{P}_{1 x}=\left.\left.\right|_{x}\langle 1 \mid 1\rangle\right|^{2}=\frac{1}{4} \\ \mathcal{P}_{0 x}=\left.\left.\right|_{x}\langle 0 \mid 1\rangle\right|^{2}=\frac{1}{2} \\ \mathcal{P}_{-1 x}=\left.\right|_{x}\left(-\left.1|1\rangle\right|^{2}=\frac{1}{4},\right. \end{array}$
as illustrated in Fig. 2.12. These experimental results can be used to determine the $S_{x}$ eigenstates in terms of the $S_{z}$ basis
$\begin{array}{l} |1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{2}|-1\rangle \\ |0\rangle_{x}=\frac{1}{\sqrt{2}}|1\rangle-\frac{1}{\sqrt{2}}|-1\rangle \\ |-1\rangle_{x}=\frac{1}{2}|1\rangle-\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{2}|-1\rangle \end{array}$"


To find the $S_{x}$ eigenstates in terms of the $S_{z}$ basis I need two more similar experiments in which the input to Sx analyzer are $0,-1$ spin particles respectively.

However I am getting a sign ambiguity while using the experimental results.

Below are two expressions which both are in line with the experiments:

* $|1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{2}|-1\rangle$
$|0\rangle_{x}=\frac{1}{\sqrt{2}}|1\rangle-\frac{1}{\sqrt{2}}|-1\rangle$
$|-1\rangle_{x}=\frac{1}{2}|1\rangle-\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{2}|-1\rangle$

* $|1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$
$|0\rangle_{x}=\frac{1}{\sqrt{2}}|1\rangle+\frac{1}{\sqrt{2}}|-1\rangle$
$|-1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$


How do we resolve this?

 

[DrClaude]

* $|1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$
$|0\rangle_{x}=\frac{1}{\sqrt{2}}|1\rangle+\frac{1}{\sqrt{2}}|-1\rangle$
$|-1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$

These states are not orthogonal.

Note that there is also some convention coming in. It is possible to find other linear combinations that satisfy the experiment, but a choice is made to recover a right-handed system of coordinates. It is also conventional to take spin along x to have real coefficients in the Sz basis.

 

[Kashmir]

These states are not orthogonal.

Note that there is also some convention coming in. It is possible to find other linear combinations that satisfy the experiment, but a choice is made to recover a right-handed system of coordinates. It is also conventional to take spin along x to have real coefficients in the Sz basis.

Here are another orthogonal vectors $|1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$

$|0\rangle_{x}=\frac{1}{\sqrt{2}}|1\rangle+\frac{1}{\sqrt{2}}|-1\rangle$

$|-1\rangle_{x}=\frac{1}{2}|1\rangle-\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$

So the other conventions as you mentioned are used to pick out a convenient set of orthogonal expressions ?

 

[Kashmir]

but a choice is made to recover a right-handed system of coordinates

Can you also please explain this?

 

[DrClaude]

Here are another orthogonal vectors $|1\rangle_{x}=\frac{1}{2}|1\rangle+\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$

$|0\rangle_{x}=\frac{1}{\sqrt{2}}|1\rangle+\frac{1}{\sqrt{2}}|-1\rangle$

$|-1\rangle_{x}=\frac{1}{2}|1\rangle-\frac{1}{\sqrt{2}}|0\rangle-\frac{1}{2}|-1\rangle$

Yes, this would be a possibility.

Can you also please explain this?

You want, for instance, that a rotation by $\pi/2$ around the y-axis will transform $\ket{1}_x$ into $\ket{1}_z$.