febbie22
- 36
- 0
Hi, I am currently doing an experiment to determine the the viscous damping coefficient (c) of a dashpot.
Where you move the position of the damper to determine the effect of the damping
but my results show that when the damper is closer to the pivot the damping increases but i thought the futher away the damper is to the beam the more damping that gets put onto the beam.
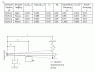
In the attachment is my result table and the figure that shows my experiment
any help would be great
Damper Positon(L2) Damper Setting Xm/Xm+1 In(Xm/Xm+1) Td Me (mass Equivalent) Equivalent Damping ce (L2/L)2 Actual Damping c (Nm/s)
50.5cm Light 1.156 0.145 0.36 4.05 3.26 0.472 6.91
50.5cm Heavy 1.33 0.288 0.34 4.05 6.86 0.472 15.5
18.3cm Light 1.031 0.031 0.34 4.05 0.74 0.062 11.9
18.3cm Heavy 1.12 0.113 0.34 4.05 2.70 0.062 43.55
Total length of beam is 73.5mm
Where you move the position of the damper to determine the effect of the damping
but my results show that when the damper is closer to the pivot the damping increases but i thought the futher away the damper is to the beam the more damping that gets put onto the beam.
In the attachment is my result table and the figure that shows my experiment
any help would be great
Damper Positon(L2) Damper Setting Xm/Xm+1 In(Xm/Xm+1) Td Me (mass Equivalent) Equivalent Damping ce (L2/L)2 Actual Damping c (Nm/s)
50.5cm Light 1.156 0.145 0.36 4.05 3.26 0.472 6.91
50.5cm Heavy 1.33 0.288 0.34 4.05 6.86 0.472 15.5
18.3cm Light 1.031 0.031 0.34 4.05 0.74 0.062 11.9
18.3cm Heavy 1.12 0.113 0.34 4.05 2.70 0.062 43.55
Total length of beam is 73.5mm
Attachments
Last edited: