How can I find the intersection point of two sticks dropped into a well?

  • MHB
  • Thread starter Ackbach
  • Start date
In summary, the depth of a well can be determined by measuring the time it takes for two sticks to hit the bottom. This can be done using the equation d=1/2 * g * t^2, where d is the depth, g is the acceleration due to gravity, and t is the time. It is important to use sticks of equal length and without significant wind resistance for accurate results. If the sticks do not intersect at the bottom, it may be necessary to repeat the experiment with longer sticks or a different method. To ensure the sticks are dropped at the same time, they can be tied together with a string or released using a pulley system. Other methods of finding the depth of a well include using a plumb
  • #1
Ackbach
Gold Member
MHB
4,155
93
Here is this week's University POTW:

-----

I have to admit this is something of an experiment. Please put aside your ego, and bear with me. You MUST record (be honest, now!) the amount of time it takes you to solve this problem. Any solution not including the time spent I will consider incorrect, and I will not publish it. Also, to be clear, I will not publish your times. If I get enough submissions, I will publish a summary of the time statistics. Indeed, if you spend time on this problem, but do not submit a solution, I'd love to have that data as well (again, I will not publish the specifics). In other words, this data I am regarding as anonymous.

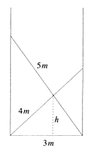
There is a well, open at the top, of diamater 3 meters. Two sticks, one of length 4 meters, and one of length 5 meters, are dropped into the well, and they land as shown in the following figure:

https://www.physicsforums.com/attachments/3735._xfImport

How high is the intersection point of the two sticks from the bottom of the well?

-----

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!
 

Attachments

  • Sticks in a Well.png
    Sticks in a Well.png
    1.8 KB · Views: 110
Physics news on Phys.org
  • #2
This problem is on pages 5 and 6 of How to Solve It: Modern Heuristics, by Michalewicz and Fogel.

MarkFL and lfdahl answered this week's POTW correctly. Here is MarkFL's solution:

I will use coordinate geometry to solve the problem. If we orient our coordinate axes such that the lower lect corner of the well is at the origin, then the 5 m stick lies along the line:

\(\displaystyle y_1=-\frac{4}{3}x+4\)

And the 4 m stick lines along the line:

\(\displaystyle y_2=\frac{\sqrt{7}}{3}x\)

Equating the two, we obtain:

\(\displaystyle -\frac{4}{3}x+4=\frac{\sqrt{7}}{3}x\)

And solving for $x$, we find:

\(\displaystyle x=\frac{12}{4+\sqrt{7}}\)

Substituting into either line (I will choose $y_2$) we then find:

\(\displaystyle h=\frac{\sqrt{7}}{3}\cdot\frac{12}{4+\sqrt{7}}=\frac{4\sqrt{7}}{4+\sqrt{7}}\)

I don't really have enough time stats to publish.
 

FAQ: How can I find the intersection point of two sticks dropped into a well?

How do I determine the depth of the well using two sticks dropped in?

The depth of the well can be calculated by measuring the time it takes for the sticks to hit the bottom of the well. Using the equation d=1/2 * g * t^2, where d is the depth, g is the acceleration due to gravity, and t is the time, the depth can be found. Make sure to use consistent units for accurate results.

Can I use any type of sticks to find the intersection point?

Yes, as long as the sticks are of equal length and are dropped at the same time. It is important to ensure that the sticks do not have any significant wind resistance, such as feathers or leaves, as this can affect the accuracy of the calculation.

What if the sticks do not intersect at the bottom of the well?

If the sticks do not intersect at the bottom of the well, it is likely that one of the sticks hit the side of the well before reaching the bottom. In this case, the calculation will not accurately determine the depth of the well. It may be necessary to repeat the experiment with longer sticks or a different method of measuring the depth.

How can I make sure the sticks are dropped at the same time?

One way to ensure the sticks are dropped at the same time is to tie them together with a string and hold onto the string before dropping them into the well. This way, when you release the string, both sticks will be released simultaneously. Another method is to use a device that can release both sticks at the same time, such as a pulley system.

Are there any other methods to find the depth of a well besides using two sticks?

Yes, there are other methods such as using a plumb line, using a weighted tape measure, or using a sonar depth finder. These methods may be more accurate and efficient than using two sticks, but they may also require more equipment and specialized knowledge.

Similar threads

MHB Is the commutator of two complex matrices nilpotent?
Replies
1
Views
2K
MHB Can a Straight Line Intersect a Curve in Four Distinct Points?
Replies
1
Views
2K
MHB What is the expected length of the shorter segment when the stick snaps?
Replies
1
Views
1K
MHB Problem of the Week # 276 - Aug 15, 2017
Replies
1
Views
2K
MHB Find the locus of a point moving so that the sum of its perpendicular distances from the four lines is constant
Replies
1
Views
2K
MHB Can three points on a circle have a distance between them of less than r^(1/3)?
Replies
1
Views
1K
MHB Problem of the Week # 142 - December 15, 2014
Replies
1
Views
1K
MHB How Do Nonempty Closed Sets Intersect in Compact Spaces?
Replies
1
Views
2K
MHB Can you find the limit of a complex function containing integrals and exponents?
Replies
1
Views
2K
MHB Do Complex Plane Medians Intersect at Triangle Centroid?
Replies
1
Views
2K

Recent Insights

Back
Top