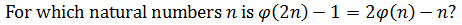SUMMARY
The discussion focuses on solving problems using Euler's Totient Function specifically for odd prime numbers. Participants analyze the function's values for specific odd primes such as 5, 7, and 11, leading to the conclusion that for any odd prime number \( n \), the value of \( \varphi(n) \) is \( n - 1 \). This is because all integers less than an odd prime \( n \) are coprime to \( n \). The discussion emphasizes understanding the function through examples to derive a general rule.
PREREQUISITES
- Understanding of Euler's Totient Function
- Basic knowledge of prime numbers
- Familiarity with number theory concepts
- Ability to perform mathematical calculations involving integers
NEXT STEPS
- Research the properties of Euler's Totient Function in detail
- Explore applications of the Totient Function in cryptography
- Learn about the generalization of the Totient Function for composite numbers
- Study the relationship between prime numbers and their totients
USEFUL FOR
Mathematicians, students of number theory, and anyone interested in the applications of Euler's Totient Function in mathematical problems and cryptography.