How Do Disjoint Intervals Solve the Inequality in POTW #409?

[anemone]

Here is this week's POTW:

-----

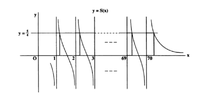
Show that the set of real numbers $x$ which satisfy the inequality $$\sum_{k=1}^{70}\dfrac{k}{x-k}\ge \dfrac{5}{4}$$ is a union of disjoint intervals, the sum of whose lengths is 1988.

-----

Remember to read the https://mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to https://mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

Hi MHB!

I have decided to extend the deadline by another week so that our members can give this problem another shot and I am looking forward to receive submissions of the solution from the members!(Happy)

 

[anemone]

No one answered to POTW #409.

Here is a suggested solution from other:

Spoiler

View attachment 9675

The function $$S(x)=\sum_{k=1}^{70}\dfrac{k}{x-k}$$ is discontinuous at $x=k$ for $k=1, 2, ..., 70$ but is continuous in the open intervals between these integers. Also, the function goes to $-\infty$ as $x$ approaches $k$ from below and to $+\infty$ as $x$ approaches $k$ from above. Thus the graph crosses the line $y=\dfrac{5}{4}$ in each of the interval $(k, k+1)$ for $k=1, 2, ..., 69$.

For $x>70$, the biggest term in $S(x)$, namely $\dfrac{70}{x-70}$, gets arbitrarily small as $x$ increases, showing that the positive $x$-axis is an asymptote. Therefore from a sketch of the graph of $y=S(x)$, we can see that the set of values of $x$ for which $S(x)\ge \dfrac{5}{4}$ consists of 70 half-open intervals, open on the left and closed on the right, which begin respectively at the integer points $x=1, 2, ..., 70$.

In fact, in the graph of $y=S(x)-\dfrac{5}{4}$, these intervals occurs on the $x$-axis as the intervals between $k$ and the root $x_k$ of the equation $S(x)-\dfrac{5}{4}=0$ which lies between $k$ and $k+1$. The length of the $k$th interval, then, is simply $x_k-k$, and the sum of all 70 intervals is

$(x_1-1)+(x_2-2)+\cdots+(x_{70}-70)=(x_1+x_2+\cdots+x_{70})-(1+2+\cdots+70)$

It remains, then, only to show that the sum of the roots of $S(x)-\dfrac{5}{4}=0$ is $1988+(1+2+\cdots+70)$.

If $S(x)-\dfrac{5}{4}=ax^{70}+bx^{69}+\cdots$, the sum of the roots is simply $-\dfrac{b}{a}$.

$S(x)-\dfrac{5}{4}=\dfrac{1}{x-1}+\dfrac{2}{x-2}+\cdots+\dfrac{70}{x-70}-\dfrac{5}{4}=0$

Clearing the fraction we get

$4(x-2)(x-3)\cdots(x-70)+4\cdot2(x-1)(x-3)\cdots(x-70)+\cdots+4\cdot70(x-1)(x-2)\cdots(x-69)-5(x-1)(x-2)\cdots(x-70)=0$

$-5x^{70}+x^{69}[4\cdot1+4\cdot2+\cdots+4\cdot70-5(-1-2-\cdots-70)]+\cdots=0$

$-5x^{70}+x^{69}[4(1+2+\cdots+70)+5(1+2+\cdots+70)]+\cdots=0$

$-5x^{70}+9(1+2+\cdots+70)x^{69}+\cdots=0$$\begin{align*}-\dfrac{b}{a}&=-\dfrac{9(1+2+\cdots+70)}{-5}\\&=(1+2+\cdots+70)+\dfrac{4(1+2+\cdots+70)}{5}\\&=(1+2+\cdots+70)+\dfrac{4}{5}\dfrac{70}{2}(1+70)\\&=(1+2+\cdots+70)+1988\text{ (Q.E.D.)}\end{align*}$