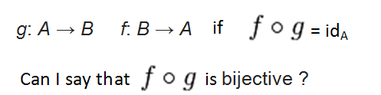Identity Function: Definition, Examples & Properties

  • Context: MHB 
  • Thread starter Thread starter dana1
  • Start date Start date
  • Tags Tags
    Function Identity
Click For Summary
SUMMARY

The discussion centers on the identity function, specifically the definition and properties of the function denoted as $id_A: A \to A$. It is established that since the identity function is a bijection, the composition of the identity function with any other function $g$ results in another bijection, represented as $f \circ g: A \to A$ where $f \circ g: a \mapsto a$. This reinforces the fundamental property of identity functions in set theory and their role in function composition.

PREREQUISITES
  • Understanding of bijections in set theory
  • Familiarity with function composition
  • Basic knowledge of mathematical notation
  • Concept of identity functions
NEXT STEPS
  • Research the properties of bijective functions in set theory
  • Learn about function composition and its implications
  • Explore examples of identity functions in various mathematical contexts
  • Study the role of identity functions in algebraic structures
USEFUL FOR

Mathematicians, educators, and students studying set theory and function properties, particularly those interested in the implications of identity functions in mathematical analysis.

dana1
Messages
4
Reaction score
0
hey,
question is attached

thanks in advance!
 

Attachments

  • question2.png
    question2.png
    3.4 KB · Views: 119
Physics news on Phys.org
dana said:
hey,
question is attached

thanks in advance!

Hi dana!

Well... since $id_A: A\to A$ is a bijection, it seems fair to me that $f \circ g: A \to A$ given by $f \circ g: a \mapsto a$ is also a bijection...
 

Similar threads

MHB Can You Help Prove This Combinatorial Identity?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Choosing from identical objects of different types
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Chernoff Bounds using importance sampling identity
  • · Replies 0 ·
Replies
0
Views
2K
Graduate Prove that points which are indistinguishable from 0 exist (using logic)
  • · Replies 17 ·
Replies
17
Views
2K
MHB Properties of the Ordinals ....
  • · Replies 1 ·
Replies
1
Views
1K
MHB Functions and Relations: Proving R is a Function from A to B
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Help understanding conditional expectation identity
  • · Replies 1 ·
Replies
1
Views
2K
MHB Finding MLE for $\theta$ of Statistical Product Model
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Question about about halting problem and this particular function
  • · Replies 54 ·
2
Replies
54
Views
6K
MHB Understanding H&J's Section 3 on Invertible & One-to-One Functions: Q&A
  • · Replies 5 ·
Replies
5
Views
2K