Infrared Divergences in QED Revisited

[David Neves]

What do you think of the following paper about QED?

https://journals.aps.org/prd/pdf/10.1103/PhysRevD.96.085002

Infrared divergences in QED revisited

Daniel Kapec, Malcolm Perry, Ana-Maria Raclariu, and Andrew Strominger
Phys. Rev. D 96, 085002 (2017) – Published 10 October 2017

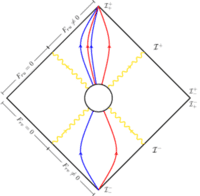
It has been found recently that the vacuum state of quantum electrodynamics (QED) is infinitely degenerate. The authors exploit this fact and show that any non-trivial scattering process in QED is necessarily accompanied by a transition among the degenerate vacua, making the scattering amplitude finite at low energy scales (infrared finite).

Recently, it has been shown that the vacuum state in QED is infinitely degenerate. Moreover, a transition among the degenerate vacua is induced in any nontrivial scattering process and determined from the associated soft factor. Conventional computations of scattering amplitudes in QED do not account for this vacuum degeneracy and therefore always give zero. This vanishing of all conventional QED amplitudes is usually attributed to infrared divergences. Here, we show that if these vacuum transitions are properly accounted for, the resulting amplitudes are nonzero and infrared finite. Our construction of finite amplitudes is mathematically equivalent to, and amounts to a physical reinterpretation of, the 1970 construction of Faddeev and Kulish.

 

[A. Neumaier]

The authors write

''Although we have phrased this result in a way that sounds new, the mathematics behind it is not new. We have merely rediscovered the 1970 formulae of Faddeev and Kulish and others, who showed that certain dressings of charges by clouds of soft photons yield IR finite scattering amplitudes. [...] While our formulae are not new, our physical interpretation is new.''

Thus it is some sort of commentary of FK that sheds new light on their construction. The driving force behing the paper is the last author, Strominger, who wrote a very useful survey arXiv:1703.05448 on the infrared structure of quantum field theories with massless bare particles.

On the other hand, the FK construction is not without problems when viewed from a rigorous perspective. For a critique see Dybalski's article arXiv:1706.09057, which treats almost rigorously a (compared to QED) simplified model.