Inscribed Quadrilateral Perpendicular Bisectors Convergence Theorem

[anemone]

Here is this week's POTW:

-----

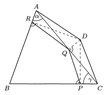
Let $ABCD$ be an inscribed quadrilateral. Let $P$, $Q$ and $R$ be the feet of the perpendiculars from $D$ to the lines $BC$, $CA$ and $AB$ respectively. Show that $PQ = QR$ if and only if the bisectors of $\angle ABC$ and $\angle ADC$ meet on $AC.$

-----

Remember to read the https://mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to https://mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

No one answered last week's POTW. (Sadface) You can refer to the suggested solution as shown below.

Spoiler

View attachment 9265

Denote in the triangle $ABC$ the angles at $A$ and $C$ by $\alpha$ and $\gamma$ respectively. $P$ and $Q$ are incident to the Thales circle of $CD$ and $\sin \angle PCQ=\sin \gamma$ or $PQ=CD\sin \gamma$.

Similarly, $QR=AD\sin \alpha$. By condition

$PQ=CD \sin \gamma=AD\sin \alpha=QR$

Rearranging and applying the sine rule for the triangle $ABC$ yields

$\dfrac{CD}{AD}=\dfrac{\sin \alpha}{\sin \gamma}=\dfrac{CB}{AB}$

By the angle bisector theorem, this holds if and only if the bisectors of $\angle ABC$ and $\angle ADC$ meet the segment $AC$ at the very same point.