Is There a Geometric Solution for the Interior Point Problem?

[Ackbach]

Here is this week's POTW:

-----

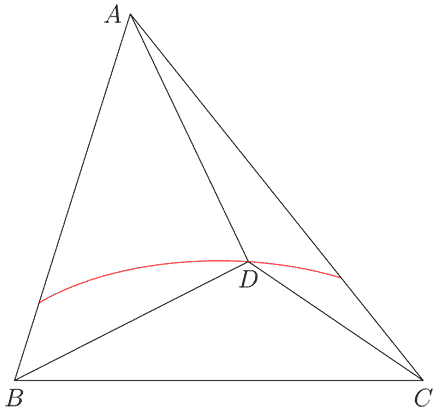
Suppose $A, B, C,$ and $D$ are points in the plane such that no three of them are collinear. If $D$ is in the interior of $\triangle ABC$, show that $| AB |+| BD |+| CD | < | AB |+| BC |+| CA |$.

Note here that $|XY|$ denotes the length of segment $XY$.

-----

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[Ackbach]

Congratulations to MarkFL and Opalg for their correct solutions. Opalg's solution, a very clever and elegant one, is below. And I do not mean to imply that Mark's is not clever, of course.

Spoiler

This is not really a rigorous proof, but it's convincing enough for me.

Suppose that $D$ moves subject to the constraint $|BD| + |CD| =$ constant. Then it will lie on an ellipse with foci at $B$ and $C$ (the red arc in the diagram). As $D$ moves along this arc, the distance $|AD|$ will have a minimum at the point where the arc is closest to $A$. But the maximum value of $|AD|$ will occur at an endpoint of the arc. This shows that the maximum value of $|AD| + |BD| + |CD|$ cannot occur in the interior of the triangle.

Now suppose that $D$ lies on one of the edges of the triangle, say $BC$. Then $|BD| + |CD| = |BC|$. As in the previous paragraph, when $D$ moves along $BC$ the distance $|AD|$ will have a minimum (at the foot of the perpendicular from $A$), but its maximum value will occur at an endpoint of $BC$.

Thus the maximum of $|AD| + |BD| + |CD|$ occurs at one of the vertices of the triangle. Its value will then be the sum of the lengths of two of the edges of the triangle, which is certainly less than the sum of the lengths of all three edges.