Linear Accelerator Length Contraction

[Orthoceras]

TL;DR

Effect of relativistic length contraction on the electron bunches in a linear accelerator?

I am trying to understand the effect of relativistic length contraction on the electron bunches in a linear accelerator. Figure B is for nonrelativistic speeds, successive cylinder lengths are progressively longer. However, wikipedia says "At speeds near the speed of light, the incremental velocity increase will be small, with the energy appearing as an increase in the mass of the particles. In portions of the accelerator where this occurs, the tubular electrode lengths will be almost constant", so it should figure D or E. I expect length contraction to occur, therefore D. However, I don't see why the the gap between bunches does not contract.

Which option is right?

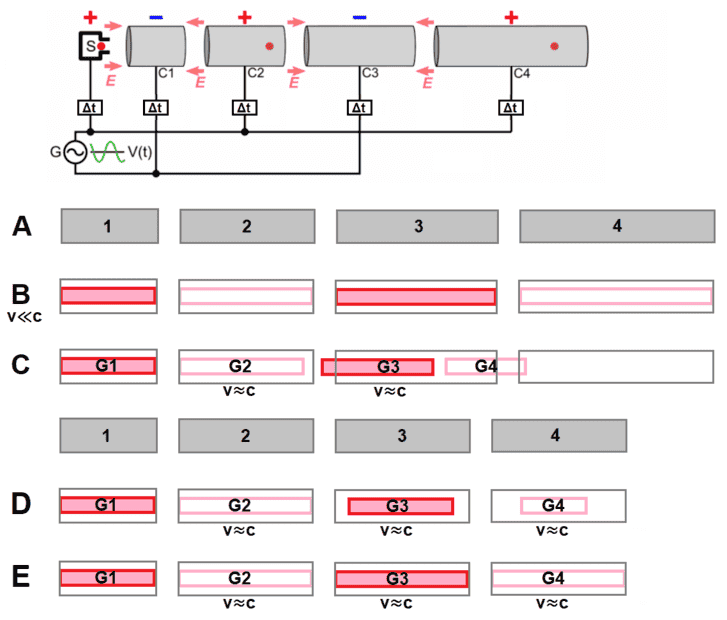
Red: electron bunches; grey: cylinders

 

[Orodruin]

Summary:: Effect of relativistic length contraction on the electron bunches in a linear accelerator?

However, I don't see why the the gap between bunches does not contract.

This has to do with how the acceleration is performed. The gap is not a rigid object (not that rigid objects exist in relativity) that maintains the same rest length. The setup is such that the distance between bunches in the instantaneous rest frame of a bunch increases during the process.