jeffer vitola
- 25
- 0
hello remember not speak English and use a translator on line,
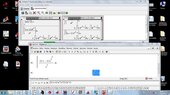
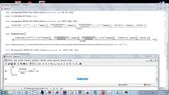
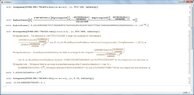
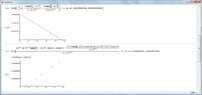
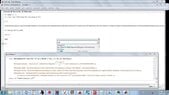
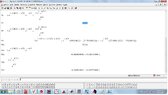
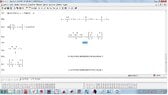
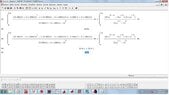
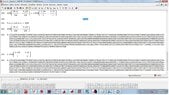
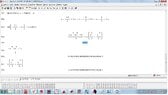
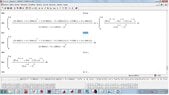
together some pictures to show some errors,from a simple integral or easy to those who are not as oscillatory integrals, when I worked and ask oscillatory integrals or approximate numerical answers, also when try plot a complex function on a small scale, the graph has cuts which is not correct because the complex function is continuous in these intervals,i want job *2 years ago texas instruments contact and wolfram alpha for these failures corrected, and I don't not *was hired as a consultant mathematician of his companies, as *i don't not they hired me, there are some mathematical problems of these programs, I do as a publication for knowledge general, I *not upload all the photos , low quality pictures so they could see on this forum. as the translator is bad clarify that I have not been hired by wolfram alpha or by texas instruments. never.*
jefferson alexander vitola (Bigsmile)
hola recuerden que yo no hablo ingles me toca usar un traductor en linea,, escribio en español you que la traduccion es muy mala. al no ser contratado como consultor matematico para texas instruments o wolfram alpha, entonces yo decidi publicar algunos errores que he encontrado desde hace you mas de 2 años entonces ahora lo voy a publicar como pasatiempo.att
jefferson alexander vitola (Bigsmile)
View attachment 917View attachment 918View attachment 919View attachment 920View attachment 921
together some pictures to show some errors,from a simple integral or easy to those who are not as oscillatory integrals, when I worked and ask oscillatory integrals or approximate numerical answers, also when try plot a complex function on a small scale, the graph has cuts which is not correct because the complex function is continuous in these intervals,i want job *2 years ago texas instruments contact and wolfram alpha for these failures corrected, and I don't not *was hired as a consultant mathematician of his companies, as *i don't not they hired me, there are some mathematical problems of these programs, I do as a publication for knowledge general, I *not upload all the photos , low quality pictures so they could see on this forum. as the translator is bad clarify that I have not been hired by wolfram alpha or by texas instruments. never.*
jefferson alexander vitola (Bigsmile)
hola recuerden que yo no hablo ingles me toca usar un traductor en linea,, escribio en español you que la traduccion es muy mala. al no ser contratado como consultor matematico para texas instruments o wolfram alpha, entonces yo decidi publicar algunos errores que he encontrado desde hace you mas de 2 años entonces ahora lo voy a publicar como pasatiempo.att
jefferson alexander vitola (Bigsmile)
View attachment 917View attachment 918View attachment 919View attachment 920View attachment 921