genxium
- 137
- 2
- TL;DR
- It was said in the paper that the just-set-free photoelectron will have an energy spread spectrum whose width change was exploited to prove that the output is in attosecond range, but some details are not clear to me.
In the 2001 paper Attosecond Metrology, the authors presented the first attosecond pulse setup and explained the measurements. This paper cites another paper quite often to mention similarities in the setup, but emphasized that they chose different observables: and only the choice made by Attosecond Metrology, "change rate of energy spectrum width", seems to be successful in proving that the generated signal has attosecond duration.
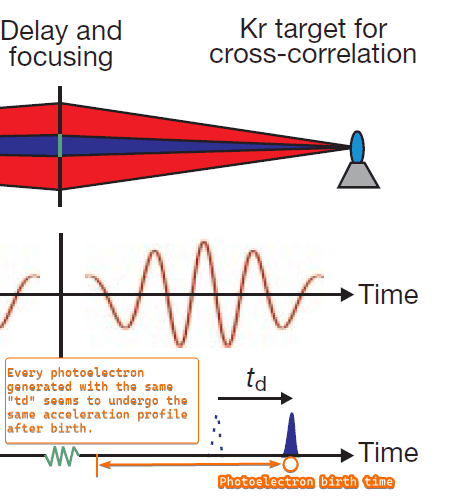
When reading these two papers, I found it difficult to understand why for a fixed "td" (the Visible laser pulse to X-ray pulse delay induced by multilayer mirror, as shown in the bottom screenshot), the detected energy of the generated photoelectron would have a spread instead of a fixed value (since the photoelectrons should've been accelerated by a same profile after getting a same initial momentum for a same "td")?
The linewidth of the X-ray is the first possible cause coming to my mind. However it's not a property induced by the presence of the Visible laser pulse and should be the same for all values of "td".
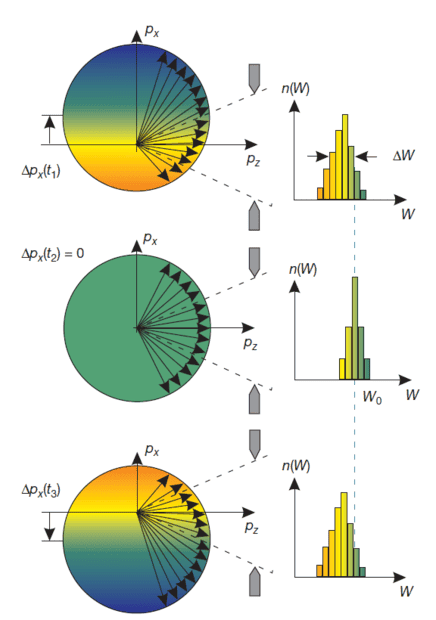
I certainly respect the Uncertainty Principle, but is it the only cause of the spread spectrum here? Later in this paper the change of energy spectrum width was up to 2 eV, meaning that ΔW itself is at least up to 2 eV which seems relatively big for uncertainty.
If it were not uncertainty that made the spread, then what is it? My only guess left is that if there's no Visible laser pulse present, after being set free the photoelectron has an initial momentum which depends on the instantaneous momentum of the electron itself when hit by X-ray pulse (which is NOT a controlled variable by the setup), but this is not explicitly told anywhere in the two papers.
Any help would be appreciated :)
(for a chosen "td", after birth the photoelectrons should've been accelerated by a same profile, so why is the detected energy spectrum so spread?)
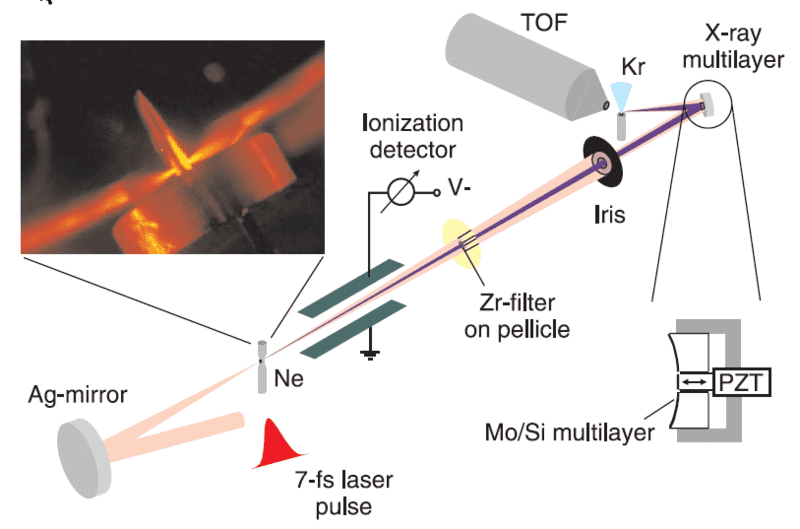
 (the setup)
(the setup)
When reading these two papers, I found it difficult to understand why for a fixed "td" (the Visible laser pulse to X-ray pulse delay induced by multilayer mirror, as shown in the bottom screenshot), the detected energy of the generated photoelectron would have a spread instead of a fixed value (since the photoelectrons should've been accelerated by a same profile after getting a same initial momentum for a same "td")?
The linewidth of the X-ray is the first possible cause coming to my mind. However it's not a property induced by the presence of the Visible laser pulse and should be the same for all values of "td".
I certainly respect the Uncertainty Principle, but is it the only cause of the spread spectrum here? Later in this paper the change of energy spectrum width was up to 2 eV, meaning that ΔW itself is at least up to 2 eV which seems relatively big for uncertainty.
If it were not uncertainty that made the spread, then what is it? My only guess left is that if there's no Visible laser pulse present, after being set free the photoelectron has an initial momentum which depends on the instantaneous momentum of the electron itself when hit by X-ray pulse (which is NOT a controlled variable by the setup), but this is not explicitly told anywhere in the two papers.
Any help would be appreciated :)
(for a chosen "td", after birth the photoelectrons should've been accelerated by a same profile, so why is the detected energy spectrum so spread?)
Last edited: