aneikei
- 16
- 0
Hello, I could some help. I've reached some sort of paradox. Ultimately I'm trying to calculate the number of pixels per inch, given a pixel size of 5177 nm and extended at a distance of .7inch (.0178 meters)
(A) (60 arcsecs * 0.0178 meters)/206268 = 5177nm pixel per arcmin
(B) 5177 * 60 = 310,620 nm per degree.
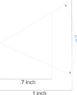
(C) tan(55)*.7 = 1 inch (thus 55 degrees = 1 inch)
(D) 310,620 * 55 = 17,084,100 nm per inch
(E) 17,084,100 nm /5177 nm = 3300ppi
However, 5177 nm = .000204 inch
and 1 inch / .000204 = 4901
Thus, 4901 x 5177nm = 25,377,450 nm per inch
25,377,450 nm /5177 nm = 4901 ppi
which is way different from 17,084,100 nm per inch
17,084,100 nm / 5177 nm = 3300 ppi
What did I do wrong? Which is correct? Thank you in advance
(A) (60 arcsecs * 0.0178 meters)/206268 = 5177nm pixel per arcmin
(B) 5177 * 60 = 310,620 nm per degree.
(C) tan(55)*.7 = 1 inch (thus 55 degrees = 1 inch)
(D) 310,620 * 55 = 17,084,100 nm per inch
(E) 17,084,100 nm /5177 nm = 3300ppi
However, 5177 nm = .000204 inch
and 1 inch / .000204 = 4901
Thus, 4901 x 5177nm = 25,377,450 nm per inch
25,377,450 nm /5177 nm = 4901 ppi
which is way different from 17,084,100 nm per inch
17,084,100 nm / 5177 nm = 3300 ppi
What did I do wrong? Which is correct? Thank you in advance