Solve the given vector problem

[chwala]

Homework Statement

This is an international past paper question- I have attached the question and the markscheme... the ms was a bit confusing for 2 marks hence my post.

Relevant Equations

vectors.

This is an international past paper question- I have attached the question and the markscheme... the ms was a bit confusing for 2 marks hence my post.

Question; interest is on part iii. only

Mark scheme solution;

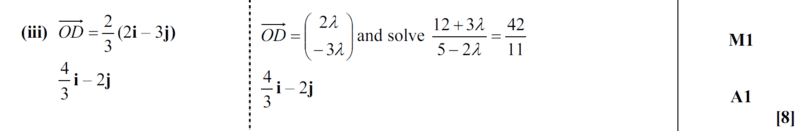My thinking;

Let

$OD=λOA$ Where $λ$ is a scalar.

$OD=λ \begin{pmatrix} 2 & \\ -3 & \\ \end{pmatrix}$

Let

$DC=κOB$ Where $κ$ is a scalar.

$DC=κ \begin{pmatrix} 11 & \\ 42 & \\ \end{pmatrix}$



$OD+DC=OC$

$λ \begin{pmatrix} 2 & \\ -3 & \\ \end{pmatrix} +κ \begin{pmatrix} 11 & \\ 42 & \\ \end{pmatrix} = \begin{pmatrix} 5 & \\ 12 & \\ \end{pmatrix}$

We end up with the simultaneous equation;

$2λ+11κ=5$
$-3λ+42κ=12$

$39λ=26$

$λ=\dfrac{2}{3}$

therefore,

$OD=\dfrac{2}{3} \begin{pmatrix} 2 & \\ -3 & \\ \end{pmatrix}=\dfrac{4}{3} i -2j$

Unless, there is something i have overlooked on the ms... the question ought to have been given more marks...cheers

Your insight highly appreciated.

 

[pasmith]

The mark scheme seems pretty consistent in awarding one mark for choosing a correct method and one mark for getting the correct answer using that method. So part (i) is worth two marks: one for observing that $\vec{AB} = \vec{OB} - \vec{OA}$ and one for doing the subtraction. Part (ii) is worth 4 marks: 2 for finding $\vec{OC}$ and 2 for calculating its length. Part (iii) is worth 2 marks: one for stating a condition which ensures that $\vec{DC}$ and $\vec{OB}$ are parallel, and one for using that condition to find $\vec{OD}$.

For part (iii), the mark scheme gives two methods to find $\vec{OD}$, each of which get the same number of marks:

• If $\vec{DC}$ and $\vec{OB}$ are parallel, then $OAB$ and $DAC$ are similar triangles. We know $\vec{AC} = \frac13 \vec{AB}$, so $\vec{AD} = \frac13\vec{AO}$ and hence $\vec{OD} = \frac23 \vec{OA}$. (This is the most obvious method if you've drawn a diagram.)
• If vectors are parallel then the ratios of the $\mathbf{i}$ and $\mathbf{j}$ components are equal; we know that $\vec{DC} = (5 - 2\lambda)\mathbf{i} + (12 + 3\lambda)\mathbf{j}$ for some $\lambda$ and we know $\vec{OB}$.

So whatever method you use to determine $\vec{OD}$, and yours involves more steps than both of these, you get one method mark and one answer mark.