Solving a system of ODEs using Runge-Kutta

[P_Sampras]

Using the 4th-order Runge-Kutta method, I have been able to successfully compute the solutions to a coupled pair of two first order differential equations using the following formula:

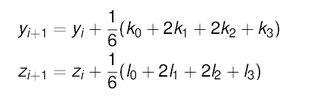
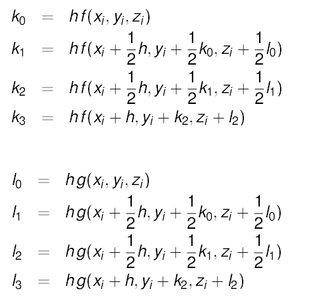
When solving systems of ODEs with more than two equations I am unsure if I am properly expanding on the above ideas.

For example I am trying to find a system of three first order equations:

da/dx = 2bc + 3a

db/dx = 4ac +11b

dc/dx = 5ab + c

Using and expanding on the equations above would I be correct in the following:

K0 = 2bc + 3a
L0 = 4ac +11b
M0 = 5ab + c

k1 = 2*(b+(L0)/2)*(c+(M0)/2) + 3*(a+(K0)/2)
L1 = 4*(a+(K0)/2)*(c+(M0)/2) + 11*(b+(L0)/2)
M1 = 5*(a+(K0)/2)*(b+(L0)/2) + (c+(M0)/2)

And so on for K2,L2,M2 etc?

Hopefully that's fairly readable.

Is this the correct approach to take or am I making a glaring error somewhere?

 

[AlephZero]

That looks rignt.

The basic idea is you first calculate all the "_0" quantities, then use them to calculate all the "_1"'s, etc.

Trying to do the calculations in a different order won't work, except in special cases and if you get lucky.