Roo2
- 44
- 0
Hello,
Upon following advice from BvU I'm starting a new thread to request help on a concrete issue I have. I have a container with 12x8 wells. Each well contains a roughly equal amount of bacteria. The bacteria are fluorescent, and I am trying to quantify their fluorescence as precisely as possible. Each strain of bacteria that I test is treated in replicate - that is, I grow it in 4 - 6 wells, depending on the experiment. To normalize for the fact that the pipetting and growth rates are not identical between wells, I am normalizing the fluorescence of the bacteria by the absorbance through the well, which scales linearly with bacterial concentration and volume of solution.
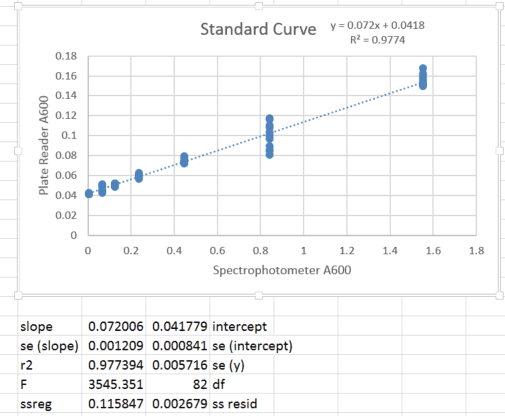
When I read absorbance, 0 bacteria (empty media) produced a non-zero value. Therefore, I made a standard curve comparing absorbance using the multiplate reader and absorbance of the same sample using a cuvette spectrophotometer, in which the pathlength is constant and measurement variability is minimal (and which is blanked such that empty media is set to 0). I performed a dilution of a bacterial culture and for each concentration, I measured once on the spectrophotometer and 12 replicate wells in the plate reader (to encompass variability in pipetting and well-to-well variation). The standard curve appears below:
For tabulating my value of interest (fluorescence normalized by absorbance), I was originally doing the following:
1. Compute mean absorbance for n replicates of a given sample
2. Background subtract the intercept of the calibration curve (0.042) and propagate the standard deviation in mean absorbance with that of the intercept (0.0008).
3. Divide mean fluorescence by the quantity computed in step 2, and propagate the standard deviations of both quantities.
However, I realized that this is probably the wrong way to go about the issue - the absorbance of a given well provides information only about that well, not any of the other replicates. Therefore, it seems that the best way to compute my value of interest would be to compute (fluorescence/absorbance) for each of n wells, and report the mean +/- s.d. of those. However, absorbance is actually the background-subtracted quantity calculated in step 2 above, except now for each individual sample's absorbance rather than the mean absorbance.
My point of confusion is in the error propagation. I am subtracting a minuend with no standard deviation (the measurement of raw absorbance for the nth sample) and a subtrahend with an associated standard deviation (the intercept of my regression). In this case, to propagate the error of the measurement, is the following strategy appropriate?
1. s.d.(absorbance) = s.d.(absorbanceraw) propagated with s.d.(regression intercept)
- result: s.d.(absorbance) = s.d.(intercept) = 0.0008 because the s.d. of a single raw absorbance measurement is 0.
2. fluorescence (f) / absorbance (a): s.d.(fluorescence) = 0 because it's a single measurement. s.d.(absorbance) is calculated in step 1.
- result: s.d.(f/a) = (f/a) * sqrt { (s.d.(f) / f)2 + (s.d.(a) / a)2} = (f/a) * sqrt{ 0 + (s.d.(a)/a)2} = f/a * (s.d.(a) / a).
3. s.d. of mean (fluorescence / absorbance) = the sum of all n values calculated in step 2 (with error propagated by addition) divided by n (s.d would then become s.d. of sum divided by n because n has no error).
This seems like the correct way to go about it, but statistics are not my forte, so I was hoping someone could take a look and catch my mistakes, if present.
Upon following advice from BvU I'm starting a new thread to request help on a concrete issue I have. I have a container with 12x8 wells. Each well contains a roughly equal amount of bacteria. The bacteria are fluorescent, and I am trying to quantify their fluorescence as precisely as possible. Each strain of bacteria that I test is treated in replicate - that is, I grow it in 4 - 6 wells, depending on the experiment. To normalize for the fact that the pipetting and growth rates are not identical between wells, I am normalizing the fluorescence of the bacteria by the absorbance through the well, which scales linearly with bacterial concentration and volume of solution.
When I read absorbance, 0 bacteria (empty media) produced a non-zero value. Therefore, I made a standard curve comparing absorbance using the multiplate reader and absorbance of the same sample using a cuvette spectrophotometer, in which the pathlength is constant and measurement variability is minimal (and which is blanked such that empty media is set to 0). I performed a dilution of a bacterial culture and for each concentration, I measured once on the spectrophotometer and 12 replicate wells in the plate reader (to encompass variability in pipetting and well-to-well variation). The standard curve appears below:
For tabulating my value of interest (fluorescence normalized by absorbance), I was originally doing the following:
1. Compute mean absorbance for n replicates of a given sample
2. Background subtract the intercept of the calibration curve (0.042) and propagate the standard deviation in mean absorbance with that of the intercept (0.0008).
3. Divide mean fluorescence by the quantity computed in step 2, and propagate the standard deviations of both quantities.
However, I realized that this is probably the wrong way to go about the issue - the absorbance of a given well provides information only about that well, not any of the other replicates. Therefore, it seems that the best way to compute my value of interest would be to compute (fluorescence/absorbance) for each of n wells, and report the mean +/- s.d. of those. However, absorbance is actually the background-subtracted quantity calculated in step 2 above, except now for each individual sample's absorbance rather than the mean absorbance.
My point of confusion is in the error propagation. I am subtracting a minuend with no standard deviation (the measurement of raw absorbance for the nth sample) and a subtrahend with an associated standard deviation (the intercept of my regression). In this case, to propagate the error of the measurement, is the following strategy appropriate?
1. s.d.(absorbance) = s.d.(absorbanceraw) propagated with s.d.(regression intercept)
- result: s.d.(absorbance) = s.d.(intercept) = 0.0008 because the s.d. of a single raw absorbance measurement is 0.
2. fluorescence (f) / absorbance (a): s.d.(fluorescence) = 0 because it's a single measurement. s.d.(absorbance) is calculated in step 1.
- result: s.d.(f/a) = (f/a) * sqrt { (s.d.(f) / f)2 + (s.d.(a) / a)2} = (f/a) * sqrt{ 0 + (s.d.(a)/a)2} = f/a * (s.d.(a) / a).
3. s.d. of mean (fluorescence / absorbance) = the sum of all n values calculated in step 2 (with error propagated by addition) divided by n (s.d would then become s.d. of sum divided by n because n has no error).
This seems like the correct way to go about it, but statistics are not my forte, so I was hoping someone could take a look and catch my mistakes, if present.
Last edited: