- #1
CSteiner
- 31
- 0
I have an extremely messy system of differential equations. Can anyone offer any ideas for a general solution?
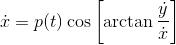
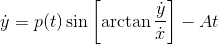
p(t) is a function of t, and A is a constant.
p(t) is a function of t, and A is a constant.
An idea would be to rewrite ##\cos \arctan \frac{\dot{y}}{\dot{x}}## as ##\frac{\dot x}{\sqrt{\dot x^2+\dot y^2}}##, and similar for the other equation. Then try to simplify it a bit.CSteiner said:I have an extremely messy system of differential equations. Can anyone offer any ideas for a general solution?
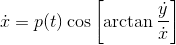
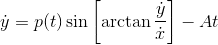
p(t) is a function of t, and A is a constant.
CSteiner said:I have an extremely messy system of differential equations. Can anyone offer any ideas for a general solution?
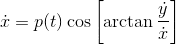
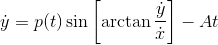
p(t) is a function of t, and A is a constant.
pasmith said:You may be best served by switching to intrinsic coordinates [itex](s, \psi)[/itex] where [tex]
\dot x = \dot s \cos\psi, \\
\dot y = \dot s \sin \psi.[/tex] Your system is then [tex]
(\dot s - p) \cos \psi = 0 \\
(\dot s - p) \sin \psi = -At.[/tex] Now either [itex]\dot s = p[/itex] or [itex]\cos \psi = 0[/itex]. The first is impossible unless [itex]A = 0[/itex]. The second requires that [itex]\dot x = 0[/itex] and [itex]\dot y = \pm p - At[/itex].
If [itex]A = 0[/itex] then [itex]\dot s = p[/itex] and [itex]\psi[/itex] can be an arbitrary function of [itex]t[/itex].
It takes time before equations render correctly but eventually they do. What are you seeing? Try a different browser or device.CSteiner said:Sorry, but it looks like something went wacky with your latex code. Could you retype it? It's hard to understand what your saying.
A system of implicit non-linear first order ODEs is a set of differential equations that describes the relationship between a set of variables and their derivatives. These equations are non-linear, meaning that the dependent variables are not directly proportional to their derivatives, and they are implicit, meaning that the dependent variables are not isolated on one side of the equation.
The main difference between implicit and explicit ODEs is the form of the equations. In explicit ODEs, the dependent variables are isolated on one side of the equation, making it easy to solve for their derivatives. In implicit ODEs, the dependent variables are not isolated, making it more difficult to solve for their derivatives. Implicit ODEs are often used when the equations are non-linear and cannot be solved explicitly.
Systems of implicit non-linear first order ODEs are used to model complex systems in physics, engineering, and other areas of science. They can describe the relationships between different variables in a system and how they change over time. These equations can then be solved numerically to understand the behavior of the system and make predictions.
There are several techniques for solving systems of implicit non-linear first order ODEs, including numerical methods such as the Euler method, the Runge-Kutta method, and the Newton-Raphson method. These methods involve approximating the solution to the equations at discrete points in time and using iterative processes to improve the accuracy of the solution.
To ensure the accuracy of their solutions, scientists often compare the results obtained from different numerical methods and use smaller time intervals to improve the accuracy of the solution. They may also use analytical techniques to check the overall behavior of the system and make sure that the numerical solutions are reasonable.