Tenenbaum & Pollard Pages 53-54: Apparently does not make sense

[xorg]

Hi. I'm reading the bookhttp://amzn.com/0486649407 ,

in self-study mode.
In page 53 and 54, below:

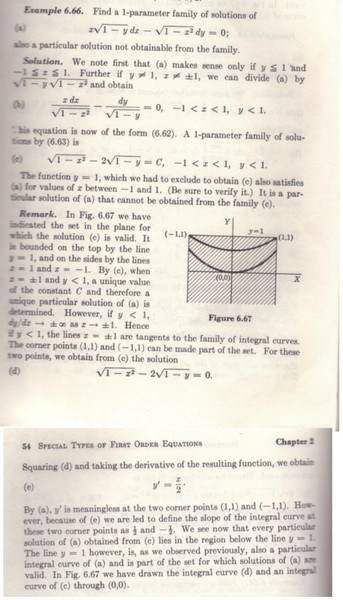
Apparently does not make sense, because, If the differential equation is:
$$ \frac{\mathrm{d}y }{\mathrm{d} x} = x\frac{\sqrt{1-y}}{\sqrt{1-x^{2}}} $$

then dy/dx = ∞ when x = 1, and y < 0
however, in Image:

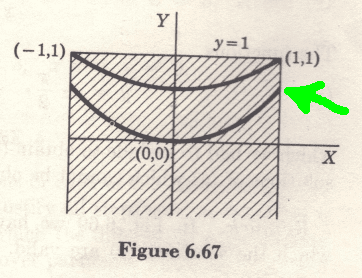
dy / dx is not ∞ in point marked in green.

Then, in this point, the graph changes radically the slope? Apparent, does not make sense, It seems that the correct curve would go up until tangent to x = 1, while the particular solution says otherwise.

Why the differential equation "fails", and the solution of the differential equation not? I did not catch that.

I am studying alone, thank you for your patience.

 

[MidgetDwarf]

There is some gap in your knowledge about what it means for a graph to have a derivative. I would advice you read a calculus book and brush up on it. This idea is a very fundamental key point in ode.

 

[Stephen Tashi]

To clarify the question: Why does the graph show a solution curve that is not asymptotic to the vertical line x = 1 ?

Apparently does not make sense, because, If the differential equation is:
$$ \frac{\mathrm{d}y }{\mathrm{d} x} = x\frac{\sqrt{1-y}}{\sqrt{1-x^{2}}} $$

then dy/dx = ∞ when x = 1, and y < 0

Did you mean "when y &lt; 1 ?

however, in Image:

dy / dx is not ∞ in point marked in green.

 

[xorg]

To clarify the question: Why does the graph show a solution curve that is not asymptotic to the vertical line x = 1 ?

Yes, if the dy/dx go to ∞ when x go to 1, then i guess in particular solution this should be the trend.
It is as if the particular solution and differential equation were conflicting.
Imagine that someone will draw the solution curves, from the dy / dx, at each point, does not match the presented solution.
However, the method of solution seems correct, that leaves me confused!

Did you mean "when y &lt; 1 ?

YES, when y<1. Sorry.

 

[slider142]

Yes, if the dy/dx go to ∞ when x go to 1, then i guess in particular solution this should be the trend.
It is as if the particular solution and differential equation were conflicting.
Imagine that someone will draw the solution curves, from the dy / dx, at each point, does not match the presented solution.
However, the method of solution seems correct, that leaves me confused!
YES, when y<1. Sorry.

You are correct: the illustration is erroneous. The solution is correct, however. If you plot the family of solutions, you will get curves with vertical tangent lines x = 1 and x = -1 when y < 1, as described by the text.
In particular, if you isolate y in the family of solutions, you will get y = \frac{1}{4}x^2 + C\sqrt{1-x^2} + \frac{3}{4} - C^2, from which you can find the explicit derivative. You can see that it is only when C = 0 that the problematic derivative of the square root at x = 1, and at x = -1, disappears.

 

[xorg]

You are correct: the illustration is erroneous. The solution is correct, however. If you plot the family of solutions, you will get curves with vertical tangent lines x = 1 and x = -1 when y < 1, as described by the text.
In particular, if you isolate y in the family of solutions, you will get y = \frac{1}{4}x^2 + C\sqrt{1-x^2} + \frac{3}{4} - C^2, from which you can find the explicit derivative. You can see that it is only when C = 0 that the problematic derivative of the square root at x = 1, and at x = -1, disappears.

Thank You!

The solution:
$$ \sqrt{1-x^{2}} - 2\sqrt{1-y} = C $$
Results:
$$ y = \frac{3}{4} + \frac{x^{2}}{4} + \frac{C\sqrt{1-x^{2}}}{2} - \frac{C^{2}}{4} $$
(in your solution, yourC = C/2)

Matlab Code

x = linspace(-1,1,1000);
clf;
grid on;
hold on;
c=0;
y=3/4+(x.^2)/4 +(c/2)*sqrt(1-(x.^2))-(c/2)^2;plot(x, y, 'r');
c=-0.5;
y=3/4+(x.^2)/4 +(c/2)*sqrt(1-(x.^2))-(c/2)^2;plot(x, y, 'b');
c=-1;
y=3/4+(x.^2)/4 +(c/2)*sqrt(1-(x.^2))-(c/2)^2;plot(x, y, 'g');

Matlab Result

c = 0
c = -0.5
c = -1


Thank you, Helped me a lot!