Discussion Overview
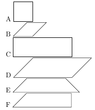
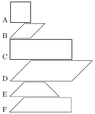
The discussion revolves around the classification and relationships between various types of plane figures, specifically squares, diamonds (rhombuses), rectangles, parallelograms, and trapezoids. Participants are examining the truth of several statements regarding set operations involving these figures.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- Some participants propose that statement (a) B U C = D is false, arguing that while diamonds and rectangles are parallelograms, not all parallelograms are diamonds or rectangles.
- Others argue that statement (b) D ∩ F = C is false, suggesting that E does not have parallel sides, which affects the intersection.
- There are claims that statement (c) D ∩ E = B is false due to E having no parallel sides.
- Some participants assert that statement (d) F "subset" D U E is correct, although this is not universally agreed upon.
- Participants also contend that statement (e) E ∩ F = B ∩ C is false, again citing the properties of E.
- Definitions of the various plane figures are requested and discussed, with some participants clarifying that "diamonds" refers to rhombuses.
Areas of Agreement / Disagreement
Participants do not reach consensus on the truth of the statements, with multiple competing views and interpretations of the relationships between the figures remaining unresolved.
Contextual Notes
Definitions of the plane figures are provided in varying degrees of clarity, and some participants express confusion regarding the properties of trapezoids and their classifications.