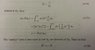Discussion Overview
The discussion revolves around understanding a specific step in the proof of the Hermitian adjoint of the operator \(\hat{D}=\partial/\partial x\) within the context of quantum mechanics, particularly focusing on the behavior of wave functions at infinity and their implications for square integrability. The scope includes theoretical aspects of quantum mechanics and mathematical reasoning related to integration by parts.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses confusion about a step in the proof related to the Hermitian adjoint and seeks clarification.
- Another suggests that the term in question is a boundary term from integration by parts, which vanishes under certain conditions.
- Some participants argue that square integrability does not necessarily imply that wave functions decay quickly enough at infinity, suggesting additional conditions may be required.
- It is proposed that for wave functions to be square-integrable and well-defined, they should approach zero at infinity, although this is contested.
- Participants discuss the relevance of physical boundary conditions and the implications for different types of wave functions, such as bound states versus free particles.
- There is mention of using the Schwarz class of functions to justify the behavior of wave functions at infinity, with some suggesting that this approach simplifies the integration process.
- One participant reflects on the need for physicists to understand distribution theory in relation to the topic.
- A later reply indicates that viewing wave functions as distributions could provide a different perspective on the problem.
- Another participant expresses gratitude for the discussion, indicating that their understanding has improved.
Areas of Agreement / Disagreement
Participants exhibit disagreement regarding the implications of square integrability and the conditions under which wave functions decay at infinity. While some suggest that certain conditions must be met, others propose that the discussion can be simplified by assuming wave functions belong to the Schwartz class. The discussion remains unresolved on these points.
Contextual Notes
Participants note that the discussion involves assumptions about the behavior of wave functions at infinity and the mathematical framework used to analyze them, including integration by parts and the properties of the Schwartz space.
Who May Find This Useful
This discussion may be useful for students and practitioners in quantum mechanics, particularly those interested in the mathematical foundations of operators and wave functions in Hilbert spaces.