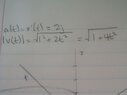ineedhelpnow
- 649
- 0
i made a calculator thread regarding this same question.
its number 7. ignore the graph on the first picture. its from the last question. the graph for this one is on the last picture. and excuse my sloppy handwriting. i was in a rush. since a(t)=2j meaning $\left\langle 0,2,0 \right\rangle$ i figured a(1) would be $\left\langle 0,2,0 \right\rangle$ but I am looking at how they did it on chegg and they did $a(1)= \left\langle 1,2,0 \right\rangle$ can someone please explain this?
View attachment 3200View attachment 3201View attachment 3202View attachment 3203
its number 7. ignore the graph on the first picture. its from the last question. the graph for this one is on the last picture. and excuse my sloppy handwriting. i was in a rush. since a(t)=2j meaning $\left\langle 0,2,0 \right\rangle$ i figured a(1) would be $\left\langle 0,2,0 \right\rangle$ but I am looking at how they did it on chegg and they did $a(1)= \left\langle 1,2,0 \right\rangle$ can someone please explain this?
View attachment 3200View attachment 3201View attachment 3202View attachment 3203
Attachments
Last edited: