Wavelet transform (CWT and DWT)

In summary, the wavelet transform is a mathematical tool used to analyze signals at different scales and resolutions. The Continuous Wavelet Transform (CWT) provides a detailed representation of a signal by allowing for continuous variations in scale and translation, making it useful for examining localized features. In contrast, the Discrete Wavelet Transform (DWT) uses a hierarchical, multiresolution approach, providing efficient data representation and compression by decomposing a signal into a set of wavelet coefficients that can capture both frequency and time information. Both transforms are widely used in various applications, including signal processing, image compression, and data analysis.
  • #1
fog37
1,569
108
Hello,
I recently got interested in wavelets. The main idea seems clear: we compute the inner product between the signal ##x(t)## and a chosen wavelet for different scale factors and translations of the wavelet over the signal. The inner product provides the coefficient for a wavelet with a specific scale factor ##a##, which is inversely related to the wavelet frequency ##f##, as we translated the wavelet over ##x(t)##.

Apparently, given a discrete signal ##x(t)##, we can calculate either its continuous wavelet transform CWT and its discrete wavelet transform (DWT). Both are transforms are discrete in the sense that the scale parameter and translation parameter have a finite numbers of values...

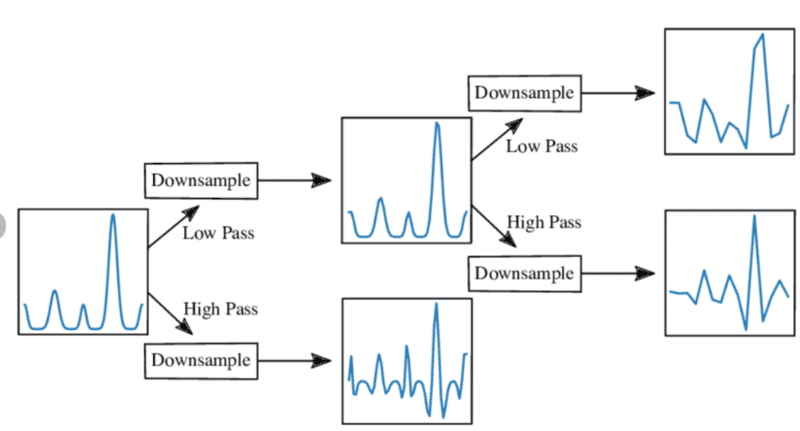
My question: the DWT can be represented as a bank of low-pass and high-pass filters. We send the signal ##x(t)## into the first pair of filter and then pass its downsampled low-pass versions into subsequent filter pairs This process apparently produces approximation and detail coefficients...I am not clear on this process...What do we do with the approximation and detail coefficients? Is the signal decomposed into a weighted sum of wavelet functions plus a weighted sum of scaling functions?

We end up with a single downsampled low-pass version of the input signal and two downsampled high-pass versions....How does that relate to obtaining a spectrogram ##F(\omega, t)## of the input signal ##x(t)##?

1709516194114.png


Thank you!
 
  • Like
Likes osilmag
Engineering news on Phys.org
  • #2
If I'm not mistaken, the coefficients are displayed over a set band of frequencies (the wavelet). Whereas, Fourier displays the amplitude of the entire spectrum of frequencies. So, your spectrogram would be limited by the wavelet.
 
  • Like
Likes fog37
  • #3
osilmag said:
If I'm not mistaken, the coefficients are displayed over a set band of frequencies (the wavelet). Whereas, Fourier displays the amplitude of the entire spectrum of frequencies. So, your spectrogram would be limited by the wavelet.
My understanding is that the detail and approximation coefficients will be the coefficients which will multiply the scaling (father) wavelets and the mother wavelets. The filters above are all bandpass filters with different frequency ranges....

I am not sure why the CWT, which is also discrete in the scale parameter ##a## and translation parameter ##\tau##, does not need the father wavelet....Any idea?
 
  • #4
I guess I would say that once you have down or up sampled the signal, you have moved on to a different wavelet, with different a and t values. I would agree with you that it is a weighted sum of wavelet functions with their scalar coefficient.
 
  • Like
Likes fog37
  • #5
osilmag said:
I guess I would say that once you have down or up sampled the signal, you have moved on to a different wavelet, with different a and t values. I would agree with you that it is a weighted sum of wavelet functions with their scalar coefficient.
Thank you!

And what is your intuition about the filters corresponding to scaled and shifted mother wavelets?
How do you factor in the father wavelet (scaling function) which is not present in the CWT that is only based on assembling the signal as a superposition of scaled and shifted mother wavelets (the daughter wavelets)?
 

FAQ: Wavelet transform (CWT and DWT)

What is the difference between Continuous Wavelet Transform (CWT) and Discrete Wavelet Transform (DWT)?

The Continuous Wavelet Transform (CWT) analyzes a signal at every possible scale and translation, providing a highly detailed time-frequency representation. In contrast, the Discrete Wavelet Transform (DWT) uses a set of discrete scales and translations, making it more computationally efficient and suitable for applications such as data compression and feature extraction.

What are the main applications of wavelet transforms?

Wavelet transforms are widely used in various fields, including signal processing, image compression (like JPEG 2000), denoising, feature extraction in machine learning, and time-frequency analysis in geophysics and biomedical signals. They are particularly effective in analyzing non-stationary signals where traditional Fourier transforms may fall short.

How do I choose the appropriate wavelet function for my analysis?

The choice of wavelet function depends on the characteristics of the signal being analyzed and the specific application. Common wavelet families include Haar, Daubechies, Symlets, and Coiflets. It is important to consider factors such as the smoothness of the wavelet, the number of vanishing moments, and how well the wavelet represents the features of interest in the signal.

Can wavelet transforms be used for real-time signal processing?

Yes, wavelet transforms can be used for real-time signal processing, particularly with the Discrete Wavelet Transform (DWT), which is computationally efficient. Applications include real-time monitoring of biomedical signals, audio processing, and telecommunications. However, the implementation must be optimized to handle the computational load effectively.

What are the advantages of using wavelet transforms over traditional Fourier transforms?

Wavelet transforms provide several advantages over traditional Fourier transforms, particularly in analyzing non-stationary signals. They offer a time-frequency representation that captures both frequency and temporal information, allowing for better localization of transient features. Additionally, wavelets can adapt to different signal characteristics, making them more versatile for various applications, such as edge detection in images and analyzing abrupt changes in signals.

Similar threads

Is my understanding of the Nyquist theorem correct?
Replies
4
Views
1K
A Regarding the Continous Wavelet Transform 'a' parameter
Replies
1
Views
1K
Wavelet transform for images cannot interpret it correctly
Replies
1
Views
1K
I What is the difference between a complete basis and an overcomplete dictionary?
Replies
5
Views
2K
How to use DWT when sample size is smaller thn filter length
Replies
1
Views
1K
Discrete Wavelets - Question on decimation of high pass
Replies
1
Views
2K
How to reconstruct a signal using the Discrete Haar Wavelet transform?
Replies
2
Views
2K
Aliasing, Continuous sinusoids and discrete sinusoids....
Replies
3
Views
1K
Find Filters for Wavelets Analysis Homework: p_k Coefficients & Relations
Replies
1
Views
2K
(Finite Impulse Response)FIR filter math by hand example
Replies
2
Views
4K

Hot Threads

Recent Insights

Back
Top