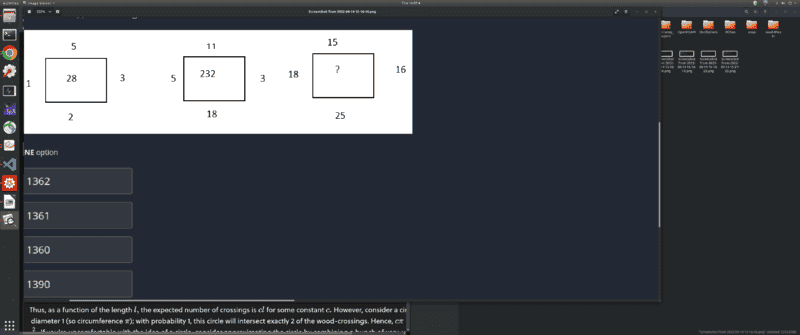
The discussion revolves around identifying a pattern for finding a missing number in a sequence, with participants exploring various mathematical approaches and reasoning related to sequences and number relationships.
The discussion includes various interpretations of the problem, with some participants sharing their thought processes and initial attempts. There is a recognition of a potential pattern, but no consensus has been reached on a definitive method for solving the problem.
Some participants mention constraints related to their initial approaches, such as the limitations of addition and the need for further exploration of number relationships.
But how? And how would I even go about doing this?fresh_42 said:
How on Earth did you know to do this? Just random guessing? What all did you check prior to this?anuttarasammyak said:
Not really. The very first thing I tried, for all of about 5 seconds, was addition, which seemed a dead end. Then I noticed that in the first problem 5 and 2 added to 7, and 3 and 1 added to 4 -- 4 * 7 = 28. The pattern was the same for the second problem.joshmccraney said:
Makes sense, thanks.Mark44 said: