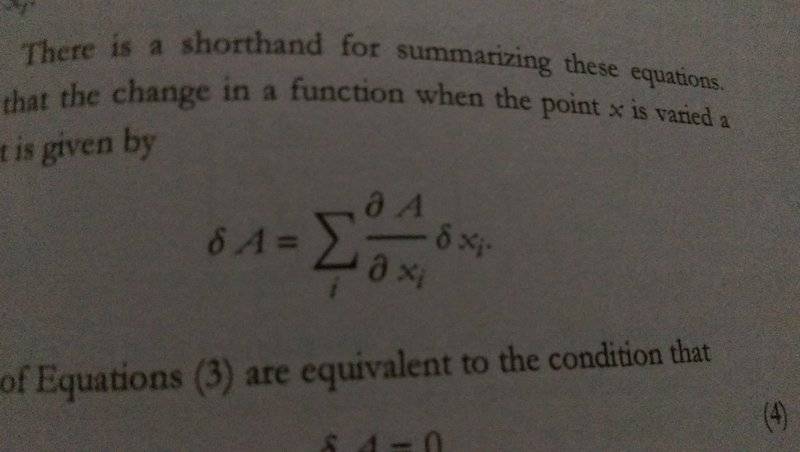SUMMARY
The discussion centers on the derivation of the equation for stationary points as presented in "The Theoretical Minimum" by Leonard Susskind. The equation describes how a small change in a function A, dependent on variables x1, ..., xn, can be expressed through its total derivative, represented as ∇A. The key equation is A(𝑥 + Δ𝑥) - A(𝑥) = ∇A · Δ𝑥 + O(∥Δ𝑥∥²), where the inner product is defined, and the term O(∥Δ𝑥∥²) represents higher-order terms that can be neglected for infinitesimally small changes.
PREREQUISITES
- Understanding of calculus, specifically total derivatives and partial derivatives.
- Familiarity with vector notation and inner products.
- Knowledge of Taylor series expansions and their applications in physics.
- Basic concepts of classical mechanics as outlined in "The Theoretical Minimum".
NEXT STEPS
- Study the concept of total derivatives in multivariable calculus.
- Learn about Taylor series and their role in approximating functions.
- Explore the implications of neglecting higher-order terms in physical equations.
- Review classical mechanics principles as discussed in "The Theoretical Minimum".
USEFUL FOR
Students of physics, mathematicians, and anyone interested in the foundational concepts of calculus and classical mechanics, particularly those studying the implications of small changes in functions.