Reallyfat
- 26
- 0
Hi everybody, I'm relatively new to particle physics. So I was reading up some stuff on high-velocity particles, and I found something on Fourmilab. The report is of a so-called OMG particle, traveling at some 0.9999999999999999999999951c. That's a ridiculously high speed, as far as I can tell. But anyways. I read that this particle was a proton, and it had an energy of around 50 joules. So I decided to use the classical physics equation:
EKinetic = m*v2*0.5
Just to test it. Needless to say, it did not work. I looked it up, and high-velocity particles have a relativistic formula where:
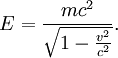
However, when I substitued my values for v and m, my energy came out as value which was to the power -10. Is there a reason that my energy value is some 10 orders of magnitude lower than it should be? And if so, could someone please guide me through the equation step-by-step so that I can work out where I went wrong?
I appreciate the responses, thanks.
EKinetic = m*v2*0.5
Just to test it. Needless to say, it did not work. I looked it up, and high-velocity particles have a relativistic formula where:
However, when I substitued my values for v and m, my energy came out as value which was to the power -10. Is there a reason that my energy value is some 10 orders of magnitude lower than it should be? And if so, could someone please guide me through the equation step-by-step so that I can work out where I went wrong?
I appreciate the responses, thanks.
Last edited: