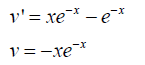SUMMARY
The integration of the function $$\int x e^{-x} \, dx$$ is solved using integration by parts, where \( u = x \) and \( dv = e^{-x} \, dx \). The correct result is \( -xe^{-x} + e^{-x} + C \), simplifying to \( -xe^{-x} \) after combining terms. The discussion highlights the efficiency of rewriting the differential equation \( y' = (x - 1)e^{-x} \) for easier integration.
PREREQUISITES
- Understanding of integration by parts
- Familiarity with exponential functions
- Basic knowledge of differential equations
- Proficiency in calculus concepts
NEXT STEPS
- Study the method of integration by parts in detail
- Explore exponential decay functions and their properties
- Learn about solving first-order differential equations
- Practice integrating various functions involving exponentials
USEFUL FOR
Students and professionals in mathematics, particularly those studying calculus and differential equations, will benefit from this discussion.