Homework Help Overview
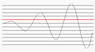
The original poster presents a problem involving the equation x*sin(x/2) - 18/pi = 0, expressing confusion about how to eliminate the sine function in order to solve for x. The context is centered around solving a transcendental equation.
Discussion Character
- Exploratory, Assumption checking, Mathematical reasoning
Approaches and Questions Raised
- Some participants suggest using Newton's method of approximation as a potential approach. Others inquire about the specifics of implementing this method and seek clarification on how to find an initial approximation.
Discussion Status
There is ongoing exploration of different methods to approach the problem, including graphical solutions and numerical methods. While some participants have shared insights on using Newton's method and graphing tools, there is no explicit consensus on a single method or solution yet.
Contextual Notes
Participants note that the function is periodic and will cross the x-axis multiple times, which may affect the choice of initial approximations for numerical methods. There is also mention of the need for a starting point in the approximation process, which remains an open question in the discussion.