- #1
jmz34
- 29
- 0
I'm just beginning to learn about Feynman diagrams and wanted to make sure I've got the correct basic understanding of QED. This is what I believe to be true right now:
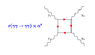
QED allows us to describe the interaction between an EM field and light/matter. The QED vertex is composed of a photon and one particle before and after the interaction. If for example an electron interacts with an EM field we can describe this interaction by saying that a virtual photon is transferred from the electron. This photon adds grad(a) to the vector potential of the field and -da/dt to the scalar potential, thus the field is unchanged.
If this is true, can we reverse the argument and say that a photon can interact with an EM field via the exchange of virtual electrons?
I may be completely wrong, just finding my lecture notes a bit difficult to comprehend.
Thanks.
QED allows us to describe the interaction between an EM field and light/matter. The QED vertex is composed of a photon and one particle before and after the interaction. If for example an electron interacts with an EM field we can describe this interaction by saying that a virtual photon is transferred from the electron. This photon adds grad(a) to the vector potential of the field and -da/dt to the scalar potential, thus the field is unchanged.
If this is true, can we reverse the argument and say that a photon can interact with an EM field via the exchange of virtual electrons?
I may be completely wrong, just finding my lecture notes a bit difficult to comprehend.
Thanks.