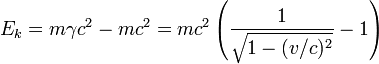Discussion Overview
The discussion revolves around the behavior of kinetic energy and force in the context of relativistic physics, particularly focusing on an electron accelerating in electric fields. Participants explore how classical concepts translate into relativistic scenarios, examining the implications of relativistic effects on kinetic energy and force equations.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant notes that classically, an electron's kinetic energy is proportional to the distance from its origin and questions if this holds at relativistic speeds.
- Another participant references a source indicating that relativistic kinetic energy and force cannot be directly derived from classical analogues by merely substituting relativistic mass.
- A different participant emphasizes the importance of energy conservation in relativity, stating that the total energy of a charged particle in an electric field remains consistent regardless of its state of motion.
- One participant introduces the concept of rapidity and its relationship with proper time, suggesting that the rate of change of rapidity is constant, which they equate to proper acceleration.
- Another participant explores the scenario of an inverse square law force, proposing a relationship between kinetic energy and the distance variable in this context, leading to a specific formulation of gamma as a function of distance.
Areas of Agreement / Disagreement
Participants express differing views on how classical mechanics translates into relativistic contexts, with no consensus reached on the exact formulations of kinetic energy and force in these scenarios.
Contextual Notes
Participants acknowledge limitations in their discussions, particularly regarding the assumptions made about force and energy conservation in relativistic contexts, and the dependence on specific definitions of terms like rapidity and proper acceleration.