- #1
Sekonda
- 207
- 0
Hello,
My question concerns the Klein-Gordon Equation under some potential of the form (and refers to a higgs-like interaction, i assume as that's what we're researching):
[tex]\delta V= \lambda \Psi^{*}\Psi[/tex]
For substitution into the Klein-Gordon equation:
[tex](\frac{\partial^2 }{\partial t^2}-\bigtriangledown ^2+m^2)\Psi=\lambda \Psi^{*}\Psi[/tex]
This is all in reference to the feynman diagram of:
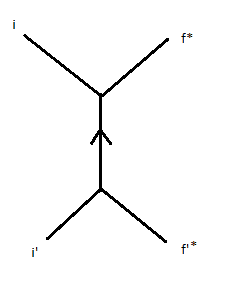
The internal line is supposed to represent some scalar mediator, and we also assume the [tex]\Psi[/tex] are 'free' states. Also there are [tex]\lambda[/tex] factors at the vertices of the feynman diagram, I believe this to be just some scaling factor of the perturbation - however I'm not sure. Also from what I've wrote the Psi's in the potential may have subscripts i' and f' but I'm not really sure why this is (they may supposed to be i and f?)
I don't understand much of this - beginning with my main issue of the form of the perturbation being what seems to be a probability density? Also I'm not really sure what interaction is exactly happening in this feyman diagram.
If what I have wrote is nonsensical, please tell me why so and I'll see if I can clear anything up. Any explanations will be appreciated!
Thanks guys,
SK.
My question concerns the Klein-Gordon Equation under some potential of the form (and refers to a higgs-like interaction, i assume as that's what we're researching):
[tex]\delta V= \lambda \Psi^{*}\Psi[/tex]
For substitution into the Klein-Gordon equation:
[tex](\frac{\partial^2 }{\partial t^2}-\bigtriangledown ^2+m^2)\Psi=\lambda \Psi^{*}\Psi[/tex]
This is all in reference to the feynman diagram of:
The internal line is supposed to represent some scalar mediator, and we also assume the [tex]\Psi[/tex] are 'free' states. Also there are [tex]\lambda[/tex] factors at the vertices of the feynman diagram, I believe this to be just some scaling factor of the perturbation - however I'm not sure. Also from what I've wrote the Psi's in the potential may have subscripts i' and f' but I'm not really sure why this is (they may supposed to be i and f?)
I don't understand much of this - beginning with my main issue of the form of the perturbation being what seems to be a probability density? Also I'm not really sure what interaction is exactly happening in this feyman diagram.
If what I have wrote is nonsensical, please tell me why so and I'll see if I can clear anything up. Any explanations will be appreciated!
Thanks guys,
SK.