- #1
d.arbitman
- 101
- 4
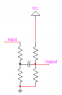
In the attached picture R1 and R2 are assumed to be equal so that they form a voltage divider. Without any signal into C1, the voltage of the base of the NPN BJT is (1/2)Vcc.
If a square wave with Vhigh = (1/2)Vcc and Vlow = 0V, and a duty cycle of 80% is fed into C1, what would be the resultant voltage ranges of the base of the transistor?
I cannot find the answer to my next question anywhere and I figure it has to do a lot with duty cycles and average signal values. If we use capacitive coupling, why must the average output signal = 0?
I hope I have provided enough information. Thank you.
If a square wave with Vhigh = (1/2)Vcc and Vlow = 0V, and a duty cycle of 80% is fed into C1, what would be the resultant voltage ranges of the base of the transistor?
I cannot find the answer to my next question anywhere and I figure it has to do a lot with duty cycles and average signal values. If we use capacitive coupling, why must the average output signal = 0?
I hope I have provided enough information. Thank you.