Solving for v_1, v_2, and v_3 with Nodal Analysis

[VinnyCee]

Find v_1,\,v_2,\,and\,v_3 in the circuit below using nodal analysis:

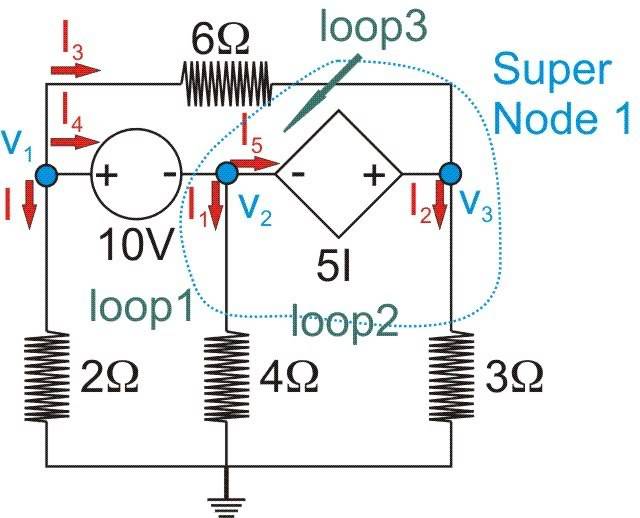
My work so far:

I\,=\,\frac{v_1}{2\Omega},\,\,I_1\,=\,\frac{v_2}{4\Omega},\,\,I_2\,=\,\frac{v_3}{3\Omega},\,\,I_3\,=\,\frac{v_1\,-\,v_3}{6\Omega}

KVL @ loop1 => -I\,(2\Omega)\,+\,10\,V\,+\,I_1(4\Omega)\,=\,0

Which equals:
-\left(\frac{v_1}{2\Omega}\right)(2\Omega)\,+\,10\,V\,+\,\left(\frac{v_2}{4\Omega}\right)(4\Omega)\,=\,0

Which equals:
-v_1\,+\,10\,V\,+\,v_2\,=\,0

KVL @ loop2 => -v_2\,-\,5\,I\,+\,v_3\,=\,0

KVL @ loop3 => -10\,V\,+\,v_1\,-\,v_3\,+\,5\,I\,=\,0

KCL @ v1 => I\,+\,I_3\,+\,I_4\,=\,0

KCL @ v2 => I_4\,=\,I_1\,+\,I_5

KCL @ v3 => I_2\,=\,I_5\,+\,I_3

KCL @ Super Node 1 => I_4\,+\,I_3\,=\,I_1\,+\,I_2

When I combine these equations to get 4 equations with 4 variables, I get the following matrix:

\left[\begin{array}{cccc|c}<br /> -1 &amp; 1 &amp; 0 &amp; 0 &amp; -10 \\<br /> 0 &amp; -1 &amp; 1 &amp; -5 &amp; 0 \\<br /> 1 &amp; 0 &amp; -1 &amp; 5 &amp; 10 \\<br /> \frac{1}{2} &amp; \frac{1}{4} &amp; \frac{1}{3} &amp; 0 &amp; 0<br /> \end{array}\right]

The columns go like this: v1, v2, v3, I, constant

But this matrix has infinite solutions! How do I solve?

 

[VinnyCee]

I figured it out!

The last variable column of the matrix can be eliminated because I\,=\,\frac{v_1}{2\Omega}

This gives the matrix:

\left[\begin{array}{ccc|c}-1 &amp; 1 &amp; 0 &amp; -10 \\-\frac{5}{2} &amp; -1 &amp; 1 &amp; 0 \\ \frac{7}{2} &amp; 0 &amp; -1 &amp; 10 \\ \frac{1}{2} &amp; \frac{1}{4} &amp; \frac{1}{3} &amp; 0 \end{array}\right]

This RREF's out to:

v_1\,=\,\frac{70}{23}\,=\,3.043\,V

v_2\,=\,-\frac{160}{23}\,=\,-6.956\,V

v_3\,=\,\frac{15}{23}\,=\,0.6522\,V\,V

NOTE: The third row of the matrix is not required!