Equivalent capacitance in series/parallel

exi

1. The problem statement, all variables and given/known data

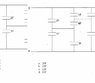
What is the equivalent capacitance for the following schematic?

Note that C1 is 11 µF, and C2 is 3 µF.



2. Relevant equations

[tex]C_{parallel} = C_1 + C_2 + C_3 + ... + C_n[/tex]

[tex]\frac{1}{C_{series}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ... + \frac{1}{C_n}[/tex]

3. The attempt at a solution

I tried the following:

1: Considered the four right-hand caps to be in parallel and add them as above, yielding 47 µF, and:

2: Added that 47 µF cap in series with the remaining 5 µF and 3 µF caps like so:

[tex]C_{eq} = \frac{1}{\frac{1}{5} + \frac{1}{47} + \frac{1}{3}} = 1.8051 \mu F[/tex]

But no go (and appropriately so, since the number seems a bit small). Where am I making a mistake?

Andrew Mason

The right-most three capacitors are in series. Find the equivalent capacitance of those three. That capacitance is then in parallel with the 4.0 uf capacitor. Find the equivalent capacitance for the parallel part. That is in series with the other two.

AM

exi

That makes a hell of a lot of sense.

I've got one remaining shot at this problem, so I would much appreciate it if someone could double-check me on this conceptually (oddly, the number still seems low at first glance, but I'm completely new to caps):

[tex]C_{rt series} = \frac{1}{\frac{1}{24} + \frac{1}{11} + \frac{1}{8}} = 3.8824 \mu F[/tex]

[tex]C_{rt parallel} = 3.8824 + 4 = 7.8824 \mu F[/tex]

[tex]C_{eq} = \frac{1}{\frac{1}{5} + \frac{1}{7.8824} + \frac{1}{3}} = 1.5147 \mu F[/tex]

proton

looks good to me

exi

Thanks for the look-over; 1.5147 is the answer.

Surprised to see it so low, but it's the answer.

kunalbhardwaj

somebody help me solve this question please
find eq capacitance when each capacitoras capaccitance C

h

vinaybrungi

hi plz anser this
this is not good see next post

Attached Thumbnails

 

vinaybrungi

plz answer this



regards

Attached Thumbnails