Redistribution of Pre-Charged Capacitors

[baseballfan_ny]

Homework Statement

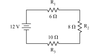
Three capacitors, of capacitances C1 = 2.0 microF , C2 = 5.0 microF , and C3 = 7.0 microF , are initially charged to 36V by connecting each, for a few instants, to a 36V battery. The battery is then removed and the charged capacitors are connected in a closed series circuit, with the positive and negative terminals joined as shown in the figure below.
a) What is the final charge on each capacitor?

Relevant Equations

Series capacitance: C = (1/C1 + 1/C2 + ... 1/Cn)

I first calculated the charge each capacitor has after its directly charged by the 36 V battery.
$Q_1 = C_1 * V = (2 \mu F) * 36 V = 72 \mu C$
$Q_2 = C_2 * V = (5 \mu F) * 36 V = 180 \mu C$
$Q_3 = C_3 * V = (7 \mu F) * 36 V = 252 \mu C$

Then these capacitors connect in series, so I thought I could create an equivalent series capacitance
$C_{eq} = (\frac 1 C_1 + \frac 1 C_2 + \frac 1 C_3)^-1$
$C_{eq} = (\frac 1 {2 \mu F} + \frac 1 {5 \mu F} + \frac 1 {7 \mu F})^-1 = 1.19 \mu F$

And the resulting on charge on the equivalent capacitor would be
$Q_{eq} = C_{eq} * V = 1.19 \mu F * 36 V = 42.7 \mu C$.

And then I thought that since we're in series the charge on each capacitor should be equivalent, so that $Q_1 = Q_2 = Q_3 = Q_{eq} = 42.7 \mu C$.

But that's wrong. Apparently each capacitor has a different charge on it? I'm not sure why, but I think it has something to do with the fact that these capacitors are pre-charged? Also I noticed $C_1$ and $C_2$ are oriented with opposite polarities; not sure if that has any impact.

 

[haruspex]

Remember there is no closed circuit, but three electrically separated sections. What will be conserved?

 

[Delta2]

I get two equations and three unknowns. Conservation of charge, KVL, what is the third equation?

 

[vela]

Conservation of charge should yield two independent equations.

 

[gneill]

Be sneaky and solve for the amount of charge that moves in the circuit. Only one KVL equation required for that. Then simply adjust the initial charges on each capacitor accordingly.

 

[baseballfan_ny]

Remember there is no closed circuit, but three electrically separated sections. What will be conserved?

Charge was my guess. And it seems to be right from the other responses.

So if I understand, the reason we can't treat these like a regular circuit is because the capacitors are all pre-charged to the same voltage (36 V) so there's no difference in potential to drive a current? I feel like I'm missing something, because if it that were the case there would be no charge that moves in the circuit.

Be sneaky and solve for the amount of charge that moves in the circuit.

How come charge moves in the circuit? My guess is it has to do something with KVL ... If each capacitor initially has 36 V then the sum of the potentials wouldn't be 0, but would be (traversing clockwise) -36 V -36 V + 36 = -36 V.

So I can get one equation by creating three variables for the final charge and using KVL. Then I get a second one from equating the sum of the initial charges with the sum of the final charges. How do you obtain a third equation?

 

[haruspex]

Charge was my guess. And it seems to be right from the other responses.

So if I understand, the reason we can't treat these like a regular circuit is because the capacitors are all pre-charged to the same voltage (36 V) so there's no difference in potential to drive a current? I feel like I'm missing something, because if it that were the case there would be no charge that moves in the circuit.
How come charge moves in the circuit? My guess is it has to do something with KVL ... If each capacitor initially has 36 V then the sum of the potentials wouldn't be 0, but would be (traversing clockwise) -36 V -36 V + 36 = -36 V.

So I can get one equation by creating three variables for the final charge and using KVL. Then I get a second one from equating the sum of the initial charges with the sum of the final charges. How do you obtain a third equation?

No, the point is that if you look at it as three electrically connected sections each consists of a wire connecting a plate of one capacitor to a plate of another. No charge can flow between sections, so the charge in each section is conserved.

 

[gneill]

How come charge moves in the circuit? My guess is it has to do something with KVL ... If each capacitor initially has 36 V then the sum of the potentials wouldn't be 0, but would be (traversing clockwise) -36 V -36 V + 36 = -36 V.

So I can get one equation by creating three variables for the final charge and using KVL. Then I get a second one from equating the sum of the initial charges with the sum of the final charges. How do you obtain a third equation?

All you need to find is the amount of charge, say "q", that has to move in the circuit in order to bring the whole into equilibrium. Current stops flowing after charge q has moved, there being no further net potential difference around the loop to drive further charge movement. That is, the sum of the potentials across each of the components around the circuit is zero. One equation will suffice to find that q. q will be the only variable, everything else being given values (initial charges on the capacitors).

So imagine that some amount of charge, q, moves in the circuit in order to bring the KVL sum around the path to zero:

Each capacitor begins with some charge on it (as you previously calculated correctly), then charge q flows around the circuit. This will have the effect of increasing some potential drops and decreasing others (if q flows out of a "+" plate it decreases the total charge on that capacitor, if it flows into a "+" plate it increases the total charge on that capacitor).

The potential across a capacitor is given by V = Q/C. So write KVL around the circuit with each capacitor's initial charge being adjusted accordingly by an amount q. Take care with the signs of the potential drops when summing them.

Solve the single resulting equation for q. That will be the amount of charge you need adjust each of the initial charges by in order to find the final charges.

 

[baseballfan_ny]

Wow, thank you so much @gneill ! That really cleared it up for me! I solved the problem and got the answer listed in the key.

I need a bit of a conceptual clarification though.

No, the point is that if you look at it as three electrically connected sections each consists of a wire connecting a plate of one capacitor to a plate of another. No charge can flow between sections, so the charge in each section is conserved.

So if I understand, the point is that the capacitors divide the circuit into three sections in which the charge remains constant, and those three sections are in between the top plates $C_2$ and $C_3$, the bottom plate of $C_2$ and the top plate of $C_1$ and the bottom plates of $C_1$ and $C_3$. No charge can flow in between sections because the capacitor plates are separated by an air gap (which is essentially an insulator with too low of a dielectric constant relative to free space)? So a circuit with a capacitor is sort of always an "open circuit?"

Also, after solving I checked the potential across each capacitor to make sure it added to zero, and got
$V_1^{'} = 14.645 V$
$V_2^{'} = 27.46 V$
$V_3^{'} = 42.1 V$

which does indeed sum close enough to zero using KVL, since $V_1^{'}$ and $V_2^{'}$ have orientations opposite $V_3^{'}$.

Current stops flowing after charge q has moved, there being no further net potential difference around the loop to drive further charge movement. That is, the sum of the potentials across each of the components around the circuit is zero.

But how come the sum of the potentials being zero implies no charge movement? Each capacitor has a different potential, shouldn't charge move between them?

In a circuit with a battery, current would only "not flow" if the potential was constant on some region. The sum of the potentials across a circuit with just batteries and resistors could still be 0 and current would still flow. Like in the image below, 0.5 A flows through each resistor and the sum of potentials overall equals 0, but current still flows since each resistor has a different potential. In the capacitor circuit in our problem, each capacitor had a different potential -- shouldn't there be some electric field between them that drives a current?

 

[gneill]

Wow, thank you so much @gneill ! That really cleared it up for me! I solved the problem and got the answer listed in the key.

Great!

I need a bit of a conceptual clarification though.So if I understand, the point is that the capacitors divide the circuit into three sections in which the charge remains constant, and those three sections are in between the top plates $C_2$ and $C_3$, the bottom plate of $C_2$ and the top plate of $C_1$ and the bottom plates of $C_1$ and $C_3$. No charge can flow in between sections because the capacitor plates are separated by an air gap (which is essentially an insulator with too low of a dielectric constant relative to free space)? So a circuit with a capacitor is sort of always an "open circuit?"

For DC, yes, after any transients have died away. In this circuit when it was assembled from pre-charged capacitors there was a "built-in" imbalance of potential drops around the circuit; a simple KVL analysis would not show a zero sum around the loop for that instant. The result is that in the instant the circuit comes together, current will flow for a very brief instant (that charge q that moves), bringing the circuit into equilibrium.

Also, after solving I checked the potential across each capacitor to make sure it added to zero, and got
$V_1^{'} = 14.645 V$
$V_2^{'} = 27.46 V$
$V_3^{'} = 42.1 V$

which does indeed sum close enough to zero using KVL, since $V_1^{'}$ and $V_2^{'}$ have orientations opposite $V_3^{'}$.

Good idea checking the results!

But how come the sum of the potentials being zero implies no charge movement? Each capacitor has a different potential, shouldn't charge move between them?

They have different potential difference across their plates, but as you noted above charges can't cross the gap in a capacitor. Plates joined by wires will share the same potential in the broader sense of potential, so no current will be made to flow in the wires between those connected plates.

Take your set of capacitor voltages and, one capacitor at a time, calculate the sum of the voltages that the other two capacitors present to it. Will any capacitor "see" a potential greater than or less that its own potential difference?

In a circuit with a battery, current would only "not flow" if the potential was constant on some region. The sum of the potentials across a circuit with just batteries and resistors could still be 0 and current would still flow. Like in the image below, 0.5 A flows through each resistor and the sum of potentials overall equals 0, but current still flows since each resistor has a different potential. In the capacitor circuit in our problem, each capacitor had a different potential -- shouldn't there be some electric field between them that drives a current?

View attachment 270799

Resistors exhibit a potential difference only when current flows through them. No current, no voltage drop. Capacitors can store charge and thus exhibit a potential difference when no current is flowing.

For your capacitor circuit current could flow if there was a path across the plates inside the capacitors. But there is not.

 

[baseballfan_ny]

For DC, yes, after any transients have died away. In this circuit when it was assembled from pre-charged capacitors there was a "built-in" imbalance of potential drops around the circuit; a simple KVL analysis would not show a zero sum around the loop for that instant. The result is that in the instant the circuit comes together, current will flow for a very brief instant (that charge q that moves), bringing the circuit into equilibrium.

Got it, makes sense.

Resistors exhibit a potential difference only when current flows through them. No current, no voltage drop. Capacitors can store charge and thus exhibit a potential difference when no current is flowing.

For your capacitor circuit current could flow if there was a path across the plates inside the capacitors. But there is not.

Also makes sense! In a circuit with resistors, there has to be a current for the voltage to sum to zero. In a circuit with capacitors, no current is needed for that.

Take your set of capacitor voltages and, one capacitor at a time, calculate the sum of the voltages that the other two capacitors present to it. Will any capacitor "see" a potential greater than or less that its own potential difference?

Tried that out; the potential of the "others" for each capacitor is the same as that of the capacitor itself, so that makes sense too!

Plates joined by wires will share the same potential in the broader sense of potential, so no current will be made to flow in the wires between those connected plates.

I think this is the point I had been missing when I first started the problem! Each capacitor plate in a given capacitor has a different potential because of the separation, but those adjoined by wires establish the same potential (like how the potential inside of a conducting object is constant because the electric field is 0 maybe). I thought I would be super cool and try to actually find what the potential at each of the 6 plates was given the conditions that those adjoined by wires are at the same potential, and came up with these equations:
$V_2^{bottom} - V_2^{top} = 27.46 V$
$V_3^{bottom} - V_3^{top} = 42.1 V$
$V_1^{bottom} - V_1^{top} = 14.645$
$V_1^{top} = V_2^{bottom}$
$V_2^{top} = V_3^{top}$
$V_3^{bottom} = V_1^{bottom}$

I spent half an hour trying to solve it and questioning my middle school education, but I think these equations have infinite solutions. I don't think I can mathematically explain that yet, but I think that it makes sense since the electric potential is kind of arbitrary and depends on your choice of a reference point. I sort of plugged and chugged possible (or potential haha get it) values for the first equation, which squeezed some values for the next potential difference equation by the equality condition, and then I subsequently assigned values to the third potential difference equation and it all worked out. I think any numbers could represent the potential, as long as their difference is equal to the observed voltage and those of connected plates are at the same potential. It just depends on the reference probably.

Anyways, none of that's really important. What matters is I finally understand the problem and can explain it to someone else -- thanks to you all! Thank you so much!

 

[haruspex]

I think these equations have infinite solutions

Potentials are always relative to some chosen zero. In principle, the choice is arbitrary, but in some contexts there are natural choices: both gravitational and electric potential are commonly taken to be zero at infinity.
In some idealised electric contexts that doesn't work, usually when charge is taken to be distributed over fewer than three dimensions, as in the present case.