Greatest shearing stress in T-Beam

[cd19]

1.

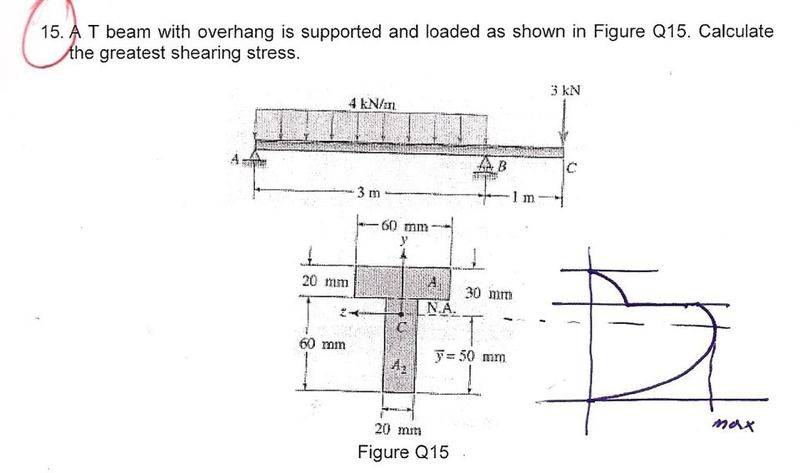
\tau = (V*Q)/(I*t)

Q=first moment of area, t=width, I= Ixx and V=shear force 3. First I found the greatest shear for to be 10Kn at point b

Then I found second moment of inertia = 1360000

Now I need to calculate for Q (first moment of area) = A*y

I need to do this for the section above the point c first (centroid)

But I'm having difficulty knowing what the value of 'y' should be in this calculation i.e the coordinates of the centroid, how to I do this?

 

[PhanthomJay]

It is easier to find Q using the area below the NA. It makes frinding the centroid of that area lower area a lot easier.

 

[cd19]

Yeah true, so if I use the bottom area the first moment of area = a*y

= 60*20 + 20*[] in the brackets I should have 'y' the centroid co-ordinates I do not know how to calculate this...

Then all I need to do is sub into equation above, How do I find 'y'

**looking at something similar it looks like the centroid co-ordinates = (10-y)*(y+(10-y)/2)

I have no Idea how this was calculated

 

[PhanthomJay]

Now I think you are getting confused. First off, the book has apparently already calculated the centroid of the T-beam cross section, C, located 50 mm from the bottom. You can arrive at that centroid location yourself by summing moment areas about the bottom, then dividing the result by the total area. Try to follow my numbers, you get y_bar = [(20)(60)(70) + (60)(20)(30)]/ [(20(60) + (60)(20)], or

y_bar = 120,000/2400 = 50 mm.

In other words, you take the area of each piece of the section and mutiply each by the distance from its own centroid to the axis you choose, add them up, then divide by total area to get the centroid (major neutral axis) of the entire section. Then I assume you then calculated 'I' correctly, I didn't check your numbers.
Now In calculating Q about C, where the stress is max, then Q is calculated by multiplying each of the rectangular areas above C by the distance from the centroid of that individual area to C, and adding up the results. OR, it is easier to look at the area below C , because only one area is involved, whereby Q = 20 x 50 X _________? If you look at finding Q using the area above C, you get the same result with a bit more work, which you should try.

 

[cd19]

Thanks for clarifying, definitely over complicated it!

What I got using the bottom area;

A\Upsilon= 20*50*20 with y being 20\tau= \frac{10000*(20*50*20)}{1.36*10^6 *(20)}=
6.87 N/mm^2 or 6.87Mpa

The question is multiple choice and one of the answers is 6.43 Mpa so I reckon its this, does this look correct?

 

[PhanthomJay]

Thanks for clarifying, definitely over complicated it!

What I got using the bottom area;

A\Upsilon= 20*50*20 with y being 20

how did you get y = 20? Using the area below C, y is the distance from the centroid of the 20 x 50 rectangle to the point C

\tau= \frac{10000*(20*50*20)}{1.36*10^6 *(20)}=
6.87 N/mm^2 or 6.87Mpa

The question is multiple choice and one of the answers is 6.43 Mpa so I reckon its this, does this look correct?

Use the correct value for Q. Otherwise, your calcs for I, V, and b look OK.

 

[cd19]

ah yeah silly mistake, so its y=25 giving me an answer of 9.19 Mpa. I've went over my calculations and they all look correct but not getting an exact value. Thanks for the help btw.

The answers; (A - 12.86), (B - 6.43), (C - 4.34), (D - 3.76), (E - 9.86)

so its E, I'm preparing for a multiple choice test, its so annoying not getting an exact value!

 

[PhanthomJay]

Yeah, I don't get 9.86 either, it's about 9.2 MPa. I solved for Q using the areas above C, and I still get Q =25,000, so I'm not sure why our answers don't agree with the 'book' answer.

edit: see below. The error is in the calculation for V.

 

[PhanthomJay]

Oops, I found the error. The max shear is not 10 kN. That's the reaction at B. The max shear at B is less than that. Draw a shear diagram or FBD left of B to solve for the correct value of V.

 

[cd19]

max shear 7 kn, 6.45mpa... thanks

 

[PhanthomJay]

Ok, looks good!