- #1
Janeabc
- 4
- 0
It is a classic 2DE quantum well problem. I do not understand few things. I haven't seen the solution anywhere on the new, so this is why i ask here.
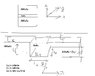
It is a quantum well - Lx is it's dimension along x-axis Ly is it's dimension along the y-axis.There is a potential as in picture let's call it Uo.
I have found from post here that the k-value is quantized. If i understood it correctly, the Kz is quantized. I am not sure what does this means. Can actually the particle in the quantum well even move along the z-axis?
What are possible values of wave-vector Kz ?As i seen in my lecture there are bound condition - so as far as i understand, Kx and Ky are quantized as well.
Kx*Lx = 2*n*Pi
Ky*Ly = 2*n*Pi
Does it change something, that in the lecture is described not single quantum well, but a periodic potential - like in a GaAs based hetero-structure.
Attachments
Last edited: